
解:(1)证明:连接OF,FC.
∵AB是直径,
∴∠BFC=90°,
∴∠AFC=90°.
又∵E是AB的中点,
∴EF=EC,
∴∠EFC=∠ECF,
∵OF=OC,
∴∠OFC=∠OCF,
∴∠OFE=∠OFC+∠EFC=∠ECF+∠FCO=∠ACB=90°.
∴OF⊥EF,
∴EF是⊙O的切线;
(2)AC
2=AF•AB
证明:∵直角△ABC中,CF⊥AB,
∴△ACF∽△ABC
∴

=

,
∴AC
2=AF•AB
(3)连接CF,BE.
∵四边形OEFB是平行四边形,
∴EF∥BC,
又∵E是AC的中点,
∴AF=BF,
∵CF⊥AB
∴AC=CB
则△ABC是等腰直角三角形.
作EM⊥AB于M.则△AEM是等腰直角三角形.
设AC=2a,则BC=2a,AE=EC=a.
∴EM=

AE=

a,
在直角△BCE中,BE=
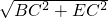
=

a.
∴sin∠ABE=

=

=

.
分析:(1)连接OF,FC,根据等腰三角形的性质证明∠EFO=∠ACB即可证得;
(2)AC
2=AF•AB,利用直角三角形的性质可以证得:△ACF∽△ABC,根据相似三角形的对应边的比相等,即可证得;
(3)连接BE,作EM⊥AB,则sin∠ABE=
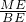
,易证得△ABC和△AEM都是等腰直角三角形,可以设AC=2a,则BE、ME都可以利用a,表示出来,从而求解.
点评:此题主要考查了圆的切线的判定定理,以及相似三角形的判定与性质,注意得到△ABC和△AEM都是等腰直角三角形是解决问题的关键.

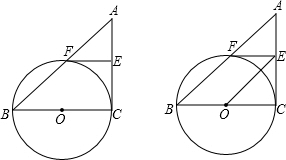 如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点F,E为AC的中点,连接FE.
如图,在△ABC中,∠C=90°,以BC为直径的⊙O交AB于点F,E为AC的中点,连接FE. 解:(1)证明:连接OF,FC.
解:(1)证明:连接OF,FC. =
= ,
, AE=
AE= a,
a,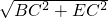 =
= a.
a. =
= =
= .
.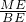 ,易证得△ABC和△AEM都是等腰直角三角形,可以设AC=2a,则BE、ME都可以利用a,表示出来,从而求解.
,易证得△ABC和△AEM都是等腰直角三角形,可以设AC=2a,则BE、ME都可以利用a,表示出来,从而求解.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为