
分析 (1)根据题意分别求出当1≤x≤8时,每平方米的售价应为4000-(8-x)×30元,当9≤x≤23时,每平方米的售价应为4000+(x-8)×50元;
(2)根据购买方案一、二求出实交房款的关系式,然后分情况讨论即可确定那种方案合算.
解答 解:(1)当1≤x≤8时,每平方米的售价应为:
y=4000-(8-x)×30=30x+3760 (元/平方米)
当9≤x≤23时,每平方米的售价应为:
y=4000+(x-8)×50=50x+3600(元/平方米).
∴y=$\left\{\begin{array}{l}{30x+3760(1≤x≤8)}\\{50x+3600(9≤x≤23)}\end{array}\right.$
(2)第十六层楼房的每平方米的价格为:50×16+3600=4400(元/平方米),
按照方案一所交房款为:W1=4400×120×(1-8%)-a=485760-a(元),
按照方案二所交房款为:W2=4400×120×(1-10%)=475200(元),
当W1>W2时,即485760-a>475200,
解得:0<a<10560,
当W1=W2时,即485760-a=475200,
解得:a=10560
当W1<W2时,即485760-a<475200,
解得:a>10560,
∴当0<a<10560时,方案二合算;当a>10560时,方案一合算.当a=10560时,方案一与方案二一样.
点评 本题考查的是用一次函数解决实际问题,读懂题目信息,找出数量关系表示出各楼层的单价以及是交房款的关系式是解题的关键.


科目:初中数学 来源: 题型:解答题
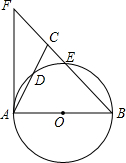 如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 29,29 | B. | 26,26 | C. | 26,29 | D. | 29,32 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向左平移1个单位,再向上平移2个单位 | |
| B. | 向左平移1个单位,再向下平移2个单位 | |
| C. | 向右平移1个单位,再向上平移2个单位 | |
| D. | 向右平移1个单位,再向下平移2个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com