
【题目】小颖根据学习函数的经验,对函数![]() 的图象与性质进行了探究,下面是小颖的探究过程,请你补充完整.
的图象与性质进行了探究,下面是小颖的探究过程,请你补充完整.
(1)列表:
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | -2 | -1 | 0 | 1 | 0 | -1 | k | … |
①![]() ____;
____;
②若![]() ,
,![]() ,
,![]() ,
,![]() 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则![]() ____;
____;
(2)描点并画出该函数的图象;
(3)①根据函数图象可得:该函数的最大值为____;
②观察函数![]() 的图象,写出该图象的两条性质________________________;_____________________;
的图象,写出该图象的两条性质________________________;_____________________;
③已知直线![]() 与函数
与函数![]() 的图象相交,则当
的图象相交,则当![]() 时,
时,![]() 的取值范围为是____.
的取值范围为是____.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某种优质蜜柚,投入市场销售时,经调查,该蜜柚每天销售量y(千克)与销售单价x(元/千克)之间符合一次函数关系,如图所示.
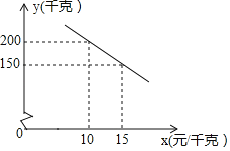
(1)求y与x的函数关系式;
(2)某农户今年共采摘该蜜柚4500千克,其保质期为40天,若以18元/千克销售,问能否在保质期内销售完这批蜜柚?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个转盘,转盘被分成4个相同的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),求下列事件的概率:

(1)指针指向绿色;
(2)指针指向红色或黄色;
(3)指针不指向红色.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】布袋里有四个小球,球表面分别标有2、3、4、6四个数字,它们的材质、形状、大小完全相同。从中随机摸出一个小球记下数字为x,再从剩下的三个球中随机摸出一个球记下数字为y,点A的坐标为(x,y).运用画树状图或列表的方法,写出A点所有可能的坐标,并求出点A在反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
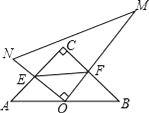
【题目】在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
A. 一定相似 B. 当E是AC中点时相似
C. 不一定相似 D. 无法判断
查看答案和解析>>
科目:初中数学 来源: 题型:
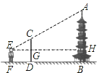
【题目】如图,小明欲测量一座古塔的高度,他拿出一根竹杆竖直插在地面上,然后自己退后,使眼睛通过竹杆的顶端刚好看到塔顶,若小明眼睛离地面![]() ,竹杆顶端离地面
,竹杆顶端离地面![]() ,小明到竹杆的距离
,小明到竹杆的距离![]() ,竹杆到塔底的距离
,竹杆到塔底的距离![]() ,求这座古塔的高度.
,求这座古塔的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
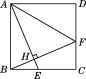
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证AE=BF;
(2)若正方形的边长是5,BE=2,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com