【题目】某种优质蜜柚，投入市场销售时，经调查，该蜜柚每天销售量y（千克）与销售单价x（元/千克）之间符合一次函数关系，如图所示．
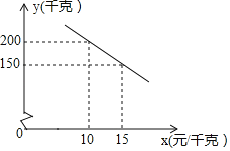
（1）求y与x的函数关系式；
（2）某农户今年共采摘该蜜柚4500千克，其保质期为40天，若以18元/千克销售，问能否在保质期内销售完这批蜜柚？请说明理由．
【答案】（1）y＝﹣10x+300；（2）能在保质期内销售完这批蜜柚，理由见解析
【解析】
（1）根据题意和函数图象中的数据，可以求得y与x的函数关系式；
（2）将x＝18代入（1）的函数解析式，求出相应的y的值，从而可以求得40天的销售量，然后与4500比较大小即可解答本题．
解：（1）设y与x的函数关系式为y＝kx+b，
将点(10,200),(15,150)代入解析式中得
解得
即y与x的函数关系式为y＝﹣10x+300；
（2）能在保质期内销售完这批蜜柚，
理由：将x＝18代入y＝﹣10x+300，得
y＝﹣10×18+300＝120，
∵120×40＝4800＞4500，
∴能在保质期内销售完这批蜜柚．
科目：初中数学 来源： 题型：
【题目】某市城区新建了一“中央商场”,该商场的第4层共分隔成了27间商铺对外招租.据预测：当每间的年租金定为8万元时，可全部租出；每间的年租金每增加0.5万元，少租出商铺1间．该公司要为租出的商铺每间每年交各种费用1万元，未租出的商铺改作其他服务（休闲）用途，每间每年需费用5 000元.
（1）当每间商铺的年租金定为10万元时,能租出_______间；
（2）当该商场第4层每间商铺的年租金定为多少万元时,该层的年收益（收益＝租金-各种费用）为199万元？
（3）当每间商铺的年租金定为_______万元时, 该“中央商场”的第4层年收益最大，最大收益为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，∠ACD是△ABC的外角，∠A=40°，BE平分∠ABC，CE平分∠ACD，且BE、CE交于点E．
（1）求∠E的度数．
（2）请猜想∠A与∠E之间的数量关系，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】黄冈市人杰地灵、山青水秀，拥有丰富的旅游资源，楚龙旅行社为吸引市民组团去大别山某风景区旅游，推出了如下收费标准：
一单位组织员工去该风景区旅游，共支付给楚龙旅行社旅游费用
元，请问该单位这次共有多少员工去旅游？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某童装店在服装销售中发现：进货价每件60元，销售价每件100元的某童装每天可售出20件
为了迎接“六一儿童节”，童装店决定采取适当的促销措施，扩大销售量，增加盈利经调查发现：如果每件童装降价1元，那么每天就可多售出2件．
如果童装店想每天销售这种童装盈利1050元，同时又要使顾客得到更多的实惠，那么每件童装应降价多少元？
每件童装降价多少元时，童装店每天可获得最大利润？最大利润是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8．在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D，E两点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小颖根据学习函数的经验，对函数
的图象与性质进行了探究，下面是小颖的探究过程，请你补充完整．
（1）列表：
x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | -2 | -1 | 0 | 1 | 0 | -1 | k | … |
①
____；
②若
，
，
，为该函数图象上不同的两点，则
____；
（2）描点并画出该函数的图象；
（3）①根据函数图象可得：该函数的最大值为____；
②观察函数的图象，写出该图象的两条性质________________________；_____________________；
③已知直线
与函数
的图象相交，则当
时，
的取值范围为是____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
