
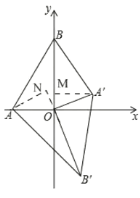
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣2,0),点B(0,2![]() ).
).

(1)直接写求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
【答案】(1)∠BAO=60°;(2)S1=S2;理由见解析;(3)S1=S2不发生变化;证明见解析.
【解析】
(1)先求出OA,OB,再用锐角三角函数即可得出结论;
(2)根据旋转的性质和直角三角形的性质可证得OA'=AA'=AO=A'B,然后根据等边△AOA'的边AO、AA'上的高相等,即可得到S1=S2;
(3)根据旋转的性质可得BO=OB',AA'=OA',再求出∠AON=∠A'OM,然后利用“角角边”证明△AON和△A'OM全等,根据全等三角形对应边相等可得AN=A'M,然后利用等底等高的三角形的面积相等证明.
解:(1)∵A(2,0),B(0,![]() ),
),
∴OA=2,OB=![]() ,
,
在Rt△AOB中,tan∠BAO=![]() ,
,
∴∠BAO=60°;
(2)S1=S2;
理由:∵∠BAO=60°,∠AOB=90°,
∴∠ABO=30°,
∴OA'=OA=![]() AB,△AOA'是等边三角形,
AB,△AOA'是等边三角形,
∴OA'=AA'=AO=A'B,
∵∠B'A'O=60°,∠A'OA=60°,
∴B'A'∥AO,
根据等边三角形的性质可得,△AOA'的边AO、AA'上的高相等,即△AB′O中AO边上高和△BA′O中BA′边上的高相等,
∴△BA'O的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2;
(3)S1=S2不发生变化;
理由:如图,过点A'作A'M⊥OB.过点A作AN⊥OB'交B'O的延长线于N,
∵△A'B'O是由△ABO绕点O旋转得到,
∴BO=OB',AO=OA',
∵∠AON+∠BON=90°,∠A'OM+∠BON=90°,
∴∠AON=∠A'OM,
在△AON和△A'OM中,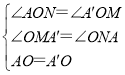 ,
,
∴△AON≌△A'OM(AAS),
∴AN=A'M,
∴△BOA'的面积和△AB'O的面积相等(等底等高的三角形的面积相等),
即S1=S2.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
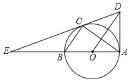
【题目】如图,AB是⊙O直径,C是半圆上一点,连接BC、AC,过点O作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=3,CE=![]() ,求线段CE、BE与劣弧BC所围成的图形面积(结果保留根号和π).
,求线段CE、BE与劣弧BC所围成的图形面积(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
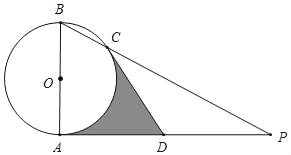
【题目】如图,AB是⊙O的直径,AP是⊙O的切线,点A为切点,BP与⊙O交于点C,点D是AP的中点,连结CD.
(1)求证:CD是⊙O的切线;
(2)若AB=2,∠P=30°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在7×7网格中,每个小正方形的边长都为1.

(1)若点A(1,3),C(2,1), ①建立适当的平面直角坐标系;②点B的坐标为( , );
(2)判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌汽车公司销售部为了制定下个月的销售计划,对 20 位销售员本月的销售量进行了 统计,绘制成如图所示的统计图,则这 20 位销售人员本月销售量的平均数、中位数、众数 分别是(单位:辆)( )

A.18.4,16,16B.18.4,20,16
C.19, 16,16D.19, 20,16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人用如图所示的两个分格均匀的转盘做游戏:分别转动两个转盘,若转盘停止后,指针指向一个数字(若指针恰好停在分格线上,则重转一次),用所指的两个数字作乘积,如果积大于10,那么甲获胜;如果积不大于10,那么乙获胜.清你解决下列问题:

(l)利用树状图(或列表)的方法表示游戏所有可能出现的结果;
(2)求甲、乙两人获胜的概率,并说明游戏是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,等边三角形ABC的边长为5,点P在线段AB上,点D在线段BC上,且△PDE是等边三角形.
(1)初步尝试:若点P与点A重合时(如图1),BD+BE= .
(2)类比探究:将点P沿AB方向移动,使AP=1,其余条件不变(如图2),试计算BD+BE的值是多少?
(3)拓展迁移:如图3,在△ABC中,AB=AC,∠BAC=70°,点P在线段AB的延长线上,点D在线段CB的延长线上,在△PDE中,PD=PE,∠DPE=70°,设BP=a,请直接写出线段BD、BE之间的数量关系(用含a的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com