
 ,0),以线段AB为边向上作菱形ABCD,且点D在y轴上.若菱形ABCD以每秒2个单位长度的速度沿射线AB滑行,直至顶点D落在x轴上时停止.设菱形落在x轴下方部分的面积为S,则表示S与滑行时间t的函数关系的图象为
,0),以线段AB为边向上作菱形ABCD,且点D在y轴上.若菱形ABCD以每秒2个单位长度的速度沿射线AB滑行,直至顶点D落在x轴上时停止.设菱形落在x轴下方部分的面积为S,则表示S与滑行时间t的函数关系的图象为




 ,0),
,0), ,
, =
=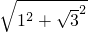 =2,
=2, =
=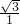 =
= ,
, =
= ,
, ,
, •2t•
•2t• t=
t= t2,
t2, [t+(t-1)•1]×
[t+(t-1)•1]× =
= t-
t- ,
, -
- (6-2t)•
(6-2t)• (6-2t)=2
(6-2t)=2 -
- (3-t)2,
(3-t)2,

科目:初中数学 来源: 题型:
 是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.
是方程x2-10x+16=0的两个根,且x1<x2,连接MC,过A、B、C三点的抛物线的顶点为N.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 4 |
| 1 |
| 8 |
| 14 |
| 3 |
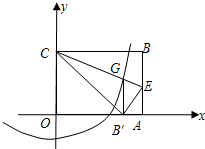 半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.
半径的圆与抛物线是否还有除G点以外的交点?若有,请找出这个交点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:
 已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.
已如:如图,在直角坐标系中,以y轴上的点C为圆心,2为半径的圆与x轴相切于原点O,AB为⊙C的直径,PA切⊙O于点A,交x轴的负半轴于点P,连接PC交OA于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.
如图:在直角坐标系中描出A(-4,-4),B(1,-4),C(2,-1),D(-3,-1)四个点.查看答案和解析>>
科目:初中数学 来源: 题型:
| a+2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com