
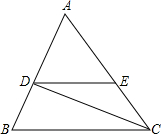
 如图,△ABC中,∠A=60°,∠B=70°,CD是∠ACB的平分线,点E在AC上,DE∥BC,则∠EDC的度数为25°.
如图,△ABC中,∠A=60°,∠B=70°,CD是∠ACB的平分线,点E在AC上,DE∥BC,则∠EDC的度数为25°. 科目:初中数学 来源: 题型:填空题
 如图,函数y=-x与函数y=-$\frac{4}{x}$的图象交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,点D.则四边形ACBD的面积为8.
如图,函数y=-x与函数y=-$\frac{4}{x}$的图象交于A,B两点,过A,B两点分别作y轴的垂线,垂足分别为点C,点D.则四边形ACBD的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
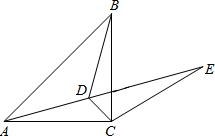 如图所示,已知点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA,则∠DCE的度数是105°.
如图所示,已知点D为等腰直角三角形ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA,则∠DCE的度数是105°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
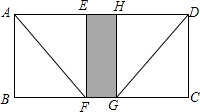 如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm
如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com