
 如图:在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(3,0)、(3,6),若经过O、A两点的抛物线y=ax2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和是$\frac{9}{2}$.
如图:在平面直角坐标系中,△OAB的顶点A、B的坐标分别为(3,0)、(3,6),若经过O、A两点的抛物线y=ax2+bx+c的顶点C落在边OB上,则图中阴影部分图形的面积和是$\frac{9}{2}$. 分析 根据抛物线抛物线y=ax2+bx+c的对称性得出阴影部分的面积实际是△ABC的面积,再根据S△ABC=$\frac{1}{2}$S△AOB,由此即可求出阴影部分的面积.
解答 解:∵抛物线y=ax2+bx+c经过O、A两点,A(3,0),B(3,6),
∴顶点C($\frac{3}{2}$,3),
∵抛物线y=ax2+bx+c的图象关于直线x=$\frac{3}{2}$对称,
∴阴影部分的面积的和实际是△ABC的面积,
∴图中阴影部分的面积的和是:$\frac{1}{2}$×$\frac{1}{2}$×3×6=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 此题考查了二次函数的性质,此题并不难,能够根据y=ax2的图象发现阴影部分与半圆面积之间的关系是解答此题的关键.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
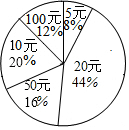 在一次救灾捐款活动中,某班50名同学人人拿出自己的零花线,有捐5元、10元、20元的,还有捐50元和100元的.如图所示的统计图反映了不同捐款数的人数比例,那么该班同学捐款的平均数、众数和中位数分别是31.2元、20元、20元.
在一次救灾捐款活动中,某班50名同学人人拿出自己的零花线,有捐5元、10元、20元的,还有捐50元和100元的.如图所示的统计图反映了不同捐款数的人数比例,那么该班同学捐款的平均数、众数和中位数分别是31.2元、20元、20元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 当测量底部不可以直接到达的物体的高度.
当测量底部不可以直接到达的物体的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com