
【题目】(知识重现)我们知道,在axN中,已知底数a,指数x,求幂N的运算叫做乘方运算.例如23=8:已知幂N,指数x,求底数a的运算叫做开方运算,例如![]() =2.
=2.
(学习新知)
现定义:如果ax=N(a0且a1),即a的x次方等于N(a0且a1),那么数x叫做以a为底N的对数(logarithm),记作x=logaN.其中a叫做对数的底数,N叫做真数,x叫做以a为底N的对数,例如log28=3,零没有对数;在实数范围内,负数没有对数.
(应用新知)
(1)选择题:在式子log5125中,真数是_______.
(2)①计算以下各对数的值:log39=_______;log327=_______.
②根据①中计算结果,请你直接写出logaM,logaN,loga(MN)之间的关系,(其中a0且a1,M0,N0).
科目:初中数学 来源: 题型:
【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位后所得直线l′的函数关系式为 . 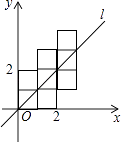
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线m经过A(4,0)、B(3,﹣![]() ),直线n经过原点且与直线m相交于D,D点的横坐标为﹣2.
),直线n经过原点且与直线m相交于D,D点的横坐标为﹣2.
(1)求直线m、n的表达式;
(2)求△OBD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是( ) 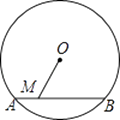
A.3≤OM≤5
B.4≤OM≤5
C.3<OM<5
D.4<OM<5
查看答案和解析>>
科目:初中数学 来源: 题型:
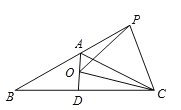
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:
①∠APO+∠DCO=30°;②△OPC是等边三角形:③AC=DO+AP;④S△ABC=S四形形AOCP.
其中正确的是_______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
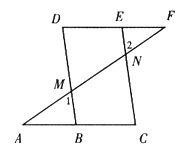
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。
证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
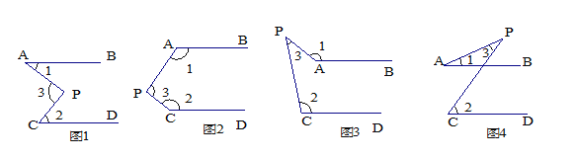
如下面四个图形中, AB∥CD.
(1)分别说出图1、图2、图3、图4中,∠1与∠2、∠3三者之间的关系.
(2)请你从中任选一个加以说明理由.
解决问题:
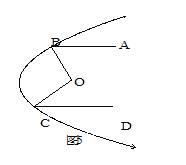
(3)如图5所示的是一探照灯灯碗的纵剖面,从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出.如果∠ABO=57°,∠DCO=44°,那么∠BOC=_______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c(a,b,c是常数,a>0)的部分图象如图所示,直线x=1是它的对称轴.若一元二次方程ax2+bx+c=0的一个根x1的取值范围是2<x1<3,则它的另一个根x2的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;
①若∠B=90°则∠F= ;
②若∠B=a,求∠F的度数(用a表示);
(2)如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com