
(1)证明:∵D为AC中点,
∴AD=CD,
∵AM∥BC,
∴∠PAC=∠ACB,
在△ADP和△CDQ中,
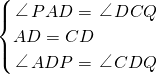
,
∴△ADP≌△CDQ(ASA),
∴PD=DQ,
又∵AD=CD,
∴四边形AQCP是平行四边形;
(2)①当Q在线段BC上,AP=QC时,以A、Q、C、P为顶点的四边形是平行四边形,
由题意得:t=6-4t,
解得:t=1.2,
当Q在C的右边时,AP=QC时,以A、Q、C、P为顶点的四边形是平行四边形,
由题意得:t=4t-6,
解得:t=2,
故答案为:1.2或2;
②(I)若CP⊥AM,则AP=3,BQ=4×3=12,点Q在C的右边,不是直角梯形.
(II)若AQ⊥BC,
∵△ABC为等腰三角形,
∴Q为BC中点,即BQ=3,
∴此时的时间为3÷4=0.75(s);
故答案为:0.75.
分析:(1)证明△ADP≌△CDQ(ASA)可得PD=DQ,又AD=CD,故四边形AQCP是平行四边形;
(2)①要分两种情况:当Q在线段BC上,AP=QC时;当Q在C的右边时,AP=QC时,粉笔根据题意算出t;
②分情况讨论:(I)若CP⊥AM,则AP=3,BQ=4×3=12,点Q在C的右边,不是直角梯形.(II)若AQ⊥BC,Q为BC中点,即BQ=3,进而得到答案.
点评:此题考查了平行四边形的判定,全等三角形的判定与性质,等腰三角形的性质,以及直角梯形,弄清题意是解本题的关键.

 如图,在△ABC中,AB=AC,射线AM∥BC,点P从点A出发沿射线AM运动,同时点Q从点B出发沿射线BC运动,设运动时间为t(s).
如图,在△ABC中,AB=AC,射线AM∥BC,点P从点A出发沿射线AM运动,同时点Q从点B出发沿射线BC运动,设运动时间为t(s). (1)证明:∵D为AC中点,
(1)证明:∵D为AC中点,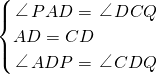 ,
,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为