
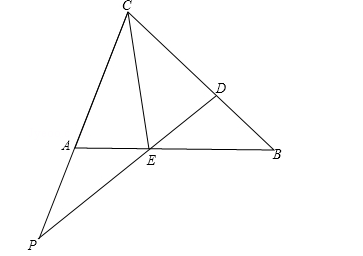
 ∠BCE;(2)若E是射线BA上一点(E不与A、B重合),连接CE,∠BEC的平分线所在直线交BC于点D,交CA所在直线于点P,∠CPD与∠BCE有什么关系?请画出图形,给出你的结论,并说明理由。
∠BCE;(2)若E是射线BA上一点(E不与A、B重合),连接CE,∠BEC的平分线所在直线交BC于点D,交CA所在直线于点P,∠CPD与∠BCE有什么关系?请画出图形,给出你的结论,并说明理由。
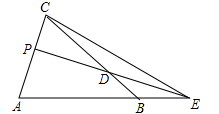
| (1)证明:∵EP平分∠BEC, ∴∠BEP=∠CEP.△ACE中,∠A+∠ACE+∠AEC=180°, ∵∠ACE=∠ACB+∠BCE,且∠A=∠ACB, ∴2∠A+2∠BEP+∠BCE=180°, ∴2(∠A+∠BEP)+∠BCE=180°, ∵∠CPD=∠A+∠BEP, ∴2∠CPD+∠BCE=180°, ∴∠CPD=90°-  ∠BCE; ∠BCE;(2)结论:∠CPD=  ∠BCE, ∠BCE,理由如下:解:设∠CAB=∠ACB=α, ∵ED平分∠BEC,∴∠BED=∠CED, 设∠BED=∠CED=β, 则∠CEB=2β, 分两种情况:i)若点E在BA上(E不与A、B重合, 如图,∵∠ACE=∠ACB-∠BCE, ∴∠ACE=α-(2α-2β)=2β-α, ∴∠BCE=∠ACB-∠ACE=α-(2β-α)=2α-2β, ∵∠CPD=∠CED-∠ACE, ∴∠CPD=β-(2β-α)=α-β, ∴∠CPD=  ∠BCE; ∠BCE;ii)若E在BA的延长线上, 如图,∵∠ACE=∠CAB-∠CEB, ∴∠ACE=α-2β, ∴∠BCE=∠ACB+∠ACE=α+(α-2β)=2α-2β, ∵∠CPD=∠ACE+∠CEP, ∴∠CPD=α-2β+β=α-β, ∴∠CPD=  ∠BCE, ∠BCE,综上,可知∠CPD=  ∠BCE。 ∠BCE。 |
   |


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com