练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，等腰梯形ABCD中，AD∥BC，BC=50，AB=20，∠B=60°，则AD=30．

    分析 首先作辅助线：过点A作AE∥CD交BC于点E，根据等腰梯形的性质，易得四边形AECD是平行四边形，根据平行四边形的对边相等，即可得AE=CD=AB=20，AD=EC，易得△ABE是等边三角形，即可求得AD的长．

    解答 解：过点A作AE∥CD交BC于点E，

    ∵AD∥BC，
    ∴四边形AECD是平行四边形，
    ∴AE=CD=AB=20，AD=EC，
    ∵∠B=60°，
    ∴BE=AB=AE=20，
    ∴AD=BC-BE=50-20=30．
    故答案为：30

    点评 此题考查了等腰梯形的性质、平行四边形的判定与性质以及等边三角形的性质．解题的关键是注意平移梯形的一腰是梯形题目中常见的辅助线．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．在平面直角坐标系中，直线y=-x+2与反比例函数y=$\frac{1}{x}$的图象有唯一公共点，若直线y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点，则b的取值范围是（　　）
    A．b＞2B．-2＜b＜2C．b＞2或b＜-2D．b＜-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列运算正确的是（　　）
    A．x2+x2=x4B．（a-b）2=a2-b2C．（-a2）3=-a6D．3a2•2a3=6a6

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知△ABC内接于⊙O，过点A作直线EF．
    （1）如图①所示，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是（至少说出两种）：∠BAE=90°或者∠EAC=∠ABC．
    （2）如图②所示，如果AB是不过圆心O的弦，且∠CAE=∠B，那么EF是⊙O的切线吗？试证明你的判断．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

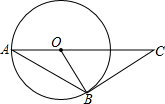    11．如图，AB是⊙O的弦，AO的延长线交过点B的⊙O的切线于点C，如果∠ABO=20°，则∠C的度数是（　　）
    A．70°B．50°C．45°D．20°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．“低碳生活，绿色出行”的理念正逐渐被人们所接受，越来越多的人选择骑自行车上下班．王叔叔某天骑自行车上班从家出发到单位过程中行进速度v（米/分钟）随时间t（分钟）变化的函数图象大致如图所示，图象由三条线段OA、AB和BC组成．设线段OC上有一动点T（t，0），直线l左侧部分的面积即为t分钟内王叔叔行进的路程s（米）．
    （1）①当t=2分钟时，速度v=200米/分钟，路程s=200米；
    ②当t=15分钟时，速度v=300米/分钟，路程s=4050米．
    （2）当0≤t≤3和3＜t≤15时，分别求出路程s（米）关于时间t（分钟）的函数解析式；
    （3）求王叔叔该天上班从家出发行进了750米时所用的时间t．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．若抛物线y=（x-m）2+（m+1）的顶点在第一象限，则m的取值范围为（　　）
    A．m＞1B．m＞0C．m＞-1D．-1＜m＜0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图，P是⊙O外一点，PA、PB分别交⊙O于C、D两点，已知$\widehat{AB}$和$\widehat{CD}$所对的圆心角分别为90°和50°，则∠P=（　　）
    A．45°B．40°C．25°D．20°

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．|-6.18|=6.18．

    查看答案和解析>>

    同步练习册答案