
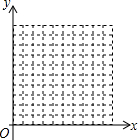
 在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,如点p从O点出发1秒时,点p的坐标为(0,1)(1,0),整数点个数为2个;点p从O点出发2秒时,点p的坐标为(0,2)(2,0),(1,1),整数点个数为3个…,当P点从点O出发10秒时,可得到整数点有11个;当P点从点O出发15秒时,可得到整数点(10,5).
在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,如点p从O点出发1秒时,点p的坐标为(0,1)(1,0),整数点个数为2个;点p从O点出发2秒时,点p的坐标为(0,2)(2,0),(1,1),整数点个数为3个…,当P点从点O出发10秒时,可得到整数点有11个;当P点从点O出发15秒时,可得到整数点(10,5). 分析 结合运动的方法以及排列组合知识得出规律“当点P出发n秒,可得到整数点n+1个,且横纵坐标之和为n”,由此规律即可得出结论.
解答 解:结合运动规律可知,当运动n秒时,横坐标可供选择的数字有:0,1,2,…,n,任取其中一个有n+1个选择,
当横坐标固定后,由运动的特性可知:横纵坐标之和为n,
∴纵坐标只有一种选法.
∴当点P出发n秒,可得到整数点n+1个,且横纵坐标之和为n.
当n=10时,可得到10+1=11个整数点;
当能得到点(10,5)时,n=10+5=15.
故答案为:11;15.
点评 本题考查了规律型的点的坐标,解题的关键是找出规律“当点P出发n秒,可得到整数点n+1个,且横纵坐标之和为n”.本题属于中档题,难度不大,解决该题型题目时,根据点P的运动方式结合前面学过的排列组合知识找出规律是关键.


科目:初中数学 来源: 题型:选择题
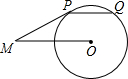 如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )
如图,PM切⊙O于点P,弦PQ∥OM,若∠OMP=30°,劣弧PQ的弧长为$\frac{π}{3}$,则线段OM的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC中,AD平分∠BAC交BC于D,CH⊥AD于H.
△ABC中,AD平分∠BAC交BC于D,CH⊥AD于H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查全国中学生心理健康现状 | |
| B. | 调查我市食品合格情况 | |
| C. | 调查你所在的班级同学的身高情况 | |
| D. | 调查桂林电视台某电视节目的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
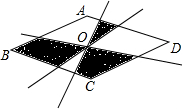 如图,四边形ABCD是菱形,点O是对角线的交点,三条直线都经过点O,图中阴影面积为24cm2,其中一对对角线长为6cm,则另一条对角线长为16cm.
如图,四边形ABCD是菱形,点O是对角线的交点,三条直线都经过点O,图中阴影面积为24cm2,其中一对对角线长为6cm,则另一条对角线长为16cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
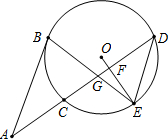 如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.
如图,AB切⊙O于点B,AD交⊙O于点C和点D,点E为$\widehat{DC}$的中点,连接OE交CD于点F,连接BE交CD于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 35 | B. | 40 | C. | 45 | D. | 55 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com