
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1 , S2 , S3 , 若S1+S2+S3=18,则正方形EFGH的面积为( ) 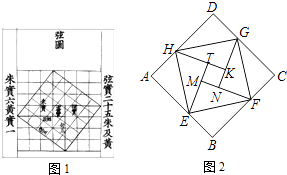
A.9
B.6
C.5
D.![]()
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF. 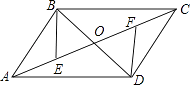
(1)求证:△BOE≌△DOF;
(2)连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
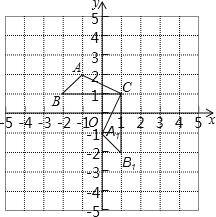
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点 逆时针旋转 度得到的,B1的坐标是 ;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一条两边互相平行的纸带折叠。
(1)若图中α=70,则β=°;
(2)探求图中α与β的数量关系;
(3)在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2),若继续沿CB边折叠,CE边恰好平分∠ACB,直接写出此时β的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A. 一个数的平方根有两个,它们互为相反数 . B. 一个数的立方根不是正数就是负数
C. 负数没有立方根 D. 如果一个数的立方根是这个数本身,那么这个数一定是-1或0或1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将若干个同样大小的小长方形纸片拼成如图形状的大长方形(小长方形纸片长为a,宽为b),请你仔细观察图形,解答下列问题: 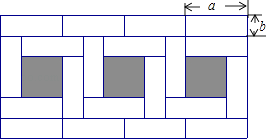
(1)a与b有怎样的关系?
(2)图中阴影部分的面积是大长方形面积的几分之几?
(3)请你仔细观察图中的一个阴影部分,根据它面积的不同表示方法写出含字母a、b的一个等式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com