
【题目】将若干个同样大小的小长方形纸片拼成如图形状的大长方形(小长方形纸片长为a,宽为b),请你仔细观察图形,解答下列问题: 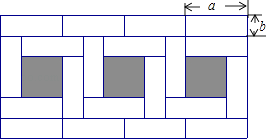
(1)a与b有怎样的关系?
(2)图中阴影部分的面积是大长方形面积的几分之几?
(3)请你仔细观察图中的一个阴影部分,根据它面积的不同表示方法写出含字母a、b的一个等式.
科目:初中数学 来源: 题型:
【题目】中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1 , S2 , S3 , 若S1+S2+S3=18,则正方形EFGH的面积为( ) 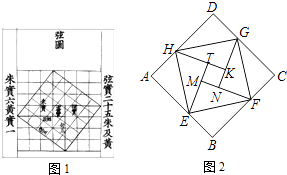
A.9
B.6
C.5
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖北襄阳第23题)
襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得自睥利润为W(万元),请直接写出年利润W(万元)关于售价(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利澜不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣ ![]() )﹣2+(1﹣
)﹣2+(1﹣ ![]() )0+(﹣5)2001×(
)0+(﹣5)2001×( ![]() )2000
)2000
(2)3a(﹣2a2)+a3
(3)(y﹣2x)(x+2y)
(4)(a﹣b+1)(a+b﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚以400米/分的速度匀速骑车5分,在原地休息了6分,然后以500米/分的速度骑回出发地,下列函数图象能表达这一过程的是( )
A.
B.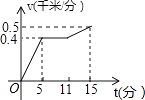
C.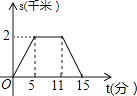
D.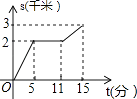
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块试验田里抽取1000个小麦穗考察它的长度(单位:厘米),从频数分布表中看到数据落在5.75~6.05之间的频数为360,于是可以估计这块试验田里长度在5.75~6.05厘米之间的麦穗约占__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)2(a+2)(b﹣4)﹣a(4a﹣3b),其中a=﹣2,b= ![]() ;
;
(2)(2a+b)(2a﹣b)﹣3(2a﹣b)2 , 其中a=﹣1,b=﹣3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2+2x-c=0中,c>0,该方程的解的情况是( ).
A.没有实数根
B.有两个不相等的实数根
C.有两个相等的实数根
D.不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com