
【题目】在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值= . 
【答案】4+2 ![]()
【解析】解:由题可得,点C在以AB为直径的⊙D上运动, 点C坐标为(x,y),可构造新的函数x+y=m,则函数与y轴交点最高处即为x+y的最大值,
此时,直线y=﹣x+m与⊙D相切,交x轴与E,如图所示,
连接OD,CD,
∵A(6,0)、B(0,2),
∴D(3,1),
∴OD= ![]() =
= ![]() ,
,
∴CD= ![]() ,
,
根据两点间的距离可得,C(3+ ![]() ,1+
,1+ ![]() ),
),
代入直线y=﹣x+m,可得
1+ ![]() =﹣(3+
=﹣(3+ ![]() )+m,
)+m,
解得m=4+2 ![]() ,
,
∴x+y的最大值为4+2 ![]() ,
,
故答案为:4+2 ![]() .
.
根据以AB为斜边在右上方作Rt△ABC,可知点C在以AB为直径的⊙D上运动,根据点C坐标为(x,y),可构造新的函数x+y=m,则函数与y轴交点最高处即为x+y的最大值,此时,直线y=﹣x+m与⊙D相切,再根据圆心点D的坐标,可得C的坐标为(3+ ![]() ,1+
,1+ ![]() ),代入直线y=﹣x+m,可得m=4+2
),代入直线y=﹣x+m,可得m=4+2 ![]() ,即可得出x+y的最大值为4+2
,即可得出x+y的最大值为4+2 ![]() .
.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)若∠ABE=15°,∠BAD=40°,则∠BED=________°;
(2)请在图中作出△BED中BD边上的高EF;
(3)若△ABC的面积为40,BD=5,则点E到BC边的距离为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场正在销售帐篷和棉被两种防寒商品,已知购买1顶帐篷和2床棉被共需300元,购买2顶帐篷和3床棉被共需510元.
(1)求1顶帐篷和1床棉被的价格各是多少元?
(2)某学校准备购买这两种防寒商品共80件,送给青海玉树灾区,要求每种商品都要购买,且帐篷的数量多于棉被的数量,但因为学校资金不足,购买总金额不能超过8500元,请问学校共有几种购买方案?(要求写出具体的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为a的正方形中挖掉一个边长为b(b<a)的小正方形,把余下的部分剪拼成一个长方形.通过计算阴影部分的面积,验证了一个等式,这个等式是( )
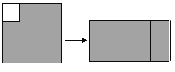
A. a2-b2=(a+b)(a-b) B. (a+b)2=a2+2ab+b2
C. (a-b)2=a2-2ab+b2 D. a2-ab=a(a-b)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于E,且AE=![]() (AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
(AD+AB).请你猜想∠1和∠2有什么数量关系?并证明你的猜想.
解:猜想: .
证明:

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过独立思考与分析后,小明和小聪开始交流解题思路如下:
小明说:解这个关于x的分式方程,得到方程的解为![]() .由题意可得
.由题意可得![]() ,所以
,所以![]() ,问题解决.
,问题解决.
小聪说:你考虑的不全面.还必须保证![]() 才行.
才行.
请回答:_______________的说法是正确的,并说明正确的理由是:__________________.
完成下列问题:
(1)已知关于x的方程![]() 的解为非负数,求m的取值范围;
的解为非负数,求m的取值范围;
(2)若关于x的分式方程![]() 无解.直接写出n的取值范围.
无解.直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( ) 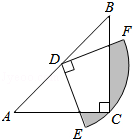
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若直线l1经过点(0,4),l2经过(3,2),且l1与l2关于x轴对称,则l1与l2的交点坐标为
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com