
【题目】阅读下列材料:
在学习“分式方程及其解法”过程中,老师提出一个问题:若关于x的分式方程![]() 的解为正数,求a的取值范围?
的解为正数,求a的取值范围?
经过独立思考与分析后,小明和小聪开始交流解题思路如下:
小明说:解这个关于x的分式方程,得到方程的解为![]() .由题意可得
.由题意可得![]() ,所以
,所以![]() ,问题解决.
,问题解决.
小聪说:你考虑的不全面.还必须保证![]() 才行.
才行.
请回答:_______________的说法是正确的,并说明正确的理由是:__________________.
完成下列问题:
(1)已知关于x的方程![]() 的解为非负数,求m的取值范围;
的解为非负数,求m的取值范围;
(2)若关于x的分式方程![]() 无解.直接写出n的取值范围.
无解.直接写出n的取值范围.
【答案】(1)见解析(2)见解析
【解析】
根据分式方程解为正数,且分母不为0判断即可;
(1)分式方程去分母转化为整式方程,由分式方程的解为非负数确定出m的范围即可.
(2) 分式方程去分母转化为整式方程,根据分式方程无解,得到有增根或整式方程无解,确定出n的范围即可.
小聪的说法是正确的,正确的理由是分式的分母不为0,故![]() ,从而
,从而![]() .
.
故答案为:小聪;分式的分母不为0,故![]() ,从而
,从而![]() .
.
(1)去分母得:m+x=2x6,
解得:x=m+6,
由分式方程的解为非负数,得到![]() ,且m+6≠3,
,且m+6≠3,
解得:![]() 且
且![]()
(2) 分式方程去分母得:32x+nx2=x+3,即(n1)x=2,
由分式方程无解,得到x3=0,即x=3,
代入整式方程得:![]()
当n1=0时,整式方程无解,此时n=1,
综上,n=1或![]()


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】2013成都)若正整数n使得在计算n+(n+1)+(n+2)的过程中,各数位均不产生进位现象,则称n为“本位数”.例如2和30是“本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
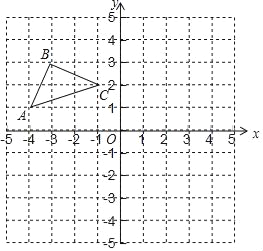
【题目】如图,在平面直角坐标系中,点O为坐标原点,已知△ABC三个定点坐标分别为A(﹣4,1),B(﹣3,3),C(﹣1,2).
(1)画出△ABC关于x轴对称的△A1B1C1,点A,B,C的对称点分别是点A1、B1、C1,直接写出点A1,B1,C1的坐标;
(2)画出点C关于y轴的对称点C2,连接C1C2,CC2,C1C,求△CC1C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O,根据下列条件,求出∠BOC的度数.
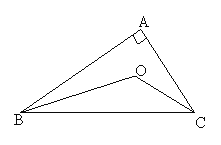
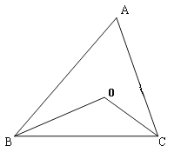
(1)已知∠ABC+∠ACB=100°,则∠BOC= .
(2)已知∠A=90°,求∠BOC的度数.
(3)从上述计算中,你能发现∠BOC与∠A的关系吗?请直接写出∠B0C与∠A的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y= ![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( ) 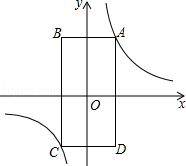
A.一直增大
B.一直减小
C.先增大后减小
D.先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何计算:
(1)如图:已知AB=9cm,BD=3cm,C为AB的中点,求线段DC的长.
![]()
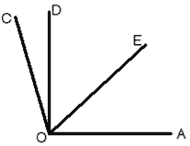
(2)如图,OE为∠AOD的平分线,∠COD=![]() ∠EOC,∠COD=15°,求:
∠EOC,∠COD=15°,求:
①∠EOC的大小;
②∠AOD的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com