Question

已知关于x的方程x²+（2m+1）x+m²+2=0有两个不相等的实数根
（1）若m为小于3的整数，则该方程的解是多少？
（2）如果A（1，y₁），B（2，y₂）是直线y=（2m-2）x-4m+7上的两点，那么你能比较y₁，y₂的大小吗？

Answer 1

【答案】分析：（1）方程有两个不相等的实数根，必须满足△=b²-4ac＞0，从而建立关于m的不等式，求出实数m的取值范围，再根据题意写一个符合条件的m的值，算出一元二次方程的解即可；
（2）根据m的取值范围确定出2m-2的范围，再根据一次函数的性质，确定出y₁，y₂的大小．
解答：解：（1）△=b²-4ac=（2m+1）²-4（m²+2）=4m-7．
由题意知：4m-7＞0，
解得：m＞，
∵m为小于3的整数，
∴可以取m=2，
把m=2代入方程得：x²+5x+6=0，
解得：x==，
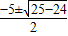
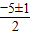
x₁=-3，x₂=-2；

（2）∵m＞，
∴2m-2＞0，
∴直线y=（2m-2）x-4m+7中y随x的增大而增大，
∵2＞1，
∴y₂＞y₁．
点评：此题主要考查了一元二次方程根的判别式，一元二次方程的解法，以及一次函数的性质，关键是根据根的判别式求出m的取值范围．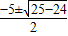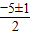