Question

有一批圆心角为90°，半径为1的扇形状下脚料，现利用这批材料截取尽可能大的正方形材料，如图有两种截取方法：方法1，如图（1）所示，正方形OPQR的顶点P、Q、R均在扇形边界上；方法2，如图（2）所示，正方形顶点C、D、E、F均在扇形边界上．图（1）、图（2）均为轴对称图形．试分别求这两种截取方法得到的正方形面积．并说明哪种截取方法得到的正方形面积更大？

Answer 1

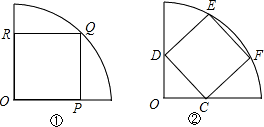
解：如图1所示：
连接OQ，设正方形OPQR的边长为x，
则在Rt△OPQ中，
OQ²=OP²+PQ²，即1²=x²+x²，
解得x=，
∴S_{四边形OPQR}=；

如图2所示，
过O作OG⊥EF，交CD于点H，连接OF，
设FG=x，
∵四边形CDEF是正方形，
∴OH⊥CD，
∴FG=CH=x，
∵∠DOC=90°，H为CD中点，
∴CH=OH，
∴OG=OH+HG=HC+CF=x+2x=3x，
在Rt△OFG中，
OF²=GF²+OG²，即1²=x²+（3x）²，
解得x=，
∴CF=2x=．
∴S_{四边形CDEF}=，
∵＞，
∴第一种方法截取的正方形的面积最大．
分析：根据题意画出图形，分别连接PQ和过O作OG⊥DE，交CF于点H，连接OF，构造直角三角形求得正方形的边长，求得正方形的面积后比较即可．由于正方形内接于扇形，故应分两种情况进行讨论．
点评：本题考查的是垂径定理及勾股定理，解答此题的关键是根据题意画出图形，作出辅助线，构造出直角三角形，再进行解答．