
 已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试证明:△ADM∽△MCP.
已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试证明:△ADM∽△MCP. 分析 欲证△ADM∽△MCP,通过观察发现两个三角形已经具备一组角对应相等,即∠D=∠C,此时,再求夹此对应角的两边对应成比例即可.
解答 证明:∵四边形ABCD是正方形,M为CD中点,
∴CM=MD=$\frac{1}{2}$AD.
∵BP=3PC,
∴PC=$\frac{1}{4}$BC=$\frac{1}{4}$AD=$\frac{1}{2}$CM.
∴$\frac{CP}{CM}$=$\frac{MD}{AD}$=$\frac{1}{2}$.
∵∠PCM=∠ADM=90°,
∴△ADM∽△MCP.
点评 本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
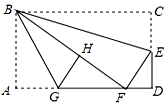 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°; ②AB:DE=AG:DF;
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°; ②AB:DE=AG:DF;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点M是反比例函数y=$\frac{1}{x}$在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=$\frac{1}{2}$A1M,△A1C1B的面积记为S1,则S1=$\frac{1}{4}$.
如图,点M是反比例函数y=$\frac{1}{x}$在第一象限内图象上的点,作MB⊥x轴于B.过点M的第一条直线交y轴于点A1,交反比例函数图象于点C1,且A1C1=$\frac{1}{2}$A1M,△A1C1B的面积记为S1,则S1=$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
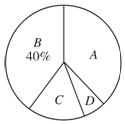 某校九年级在中考体育考试前后进行了最后一次立定跳远测试,小明同学从学年200名男生测试的成绩中随机抽取了50个,按A、B、C、D四个等级进行统计,并将统计的结果绘制成了如下的统计表和扇形图:
某校九年级在中考体育考试前后进行了最后一次立定跳远测试,小明同学从学年200名男生测试的成绩中随机抽取了50个,按A、B、C、D四个等级进行统计,并将统计的结果绘制成了如下的统计表和扇形图:| 等级 | A | B | C | D | 合计 | |||
| 成绩(分) | 10 | 9 | 8 | 7 | 6 | 5 | 5以下 | |
| 频数(人) | 6 | 13 | m | 8 | 6 | n | 3 | 50 |
| 频率 | 0.12 | 0.26 | p | 0.16 | 0.12 | q | 0.06 | 1.00 |
查看答案和解析>>
科目:初中数学 来源:2017届山东泰安市中考二模数学试卷(解析版) 题型:单选题
已知边长为a的正方形的面积为8,则下列说法中,错误的是( )
A. a是无理数 B. a是方程x2﹣3=0的解
C. a是8的算术平方根 D. 3<a<4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com