已知等腰三角形中,AB=AC,一腰上的中线BD把这个三角形的周长分成15cm和6cm两部分,求这个等腰三角形的底边的长.

解:如图,根据题意得:AB=AC,AD=CD,
设BC=xcm,AD=CD=ycm,
则AB=AC=2ycm,
①若AB+AD=15cm,BC+CD=6cm,
则

,
解得:
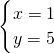
,
即AB=AC=10cm,BC=1cm;
②若AB+AD=6cm,BC+CD=15cm,
则

,
解得:

,
即AB=AC=4cm,BC=13cm,
∵4+4=8<13,不能组成三角形,舍去;
∴这个等腰三角形的底边的长为1cm.
分析:已知腰上的中线BD将这个等腰三角形的周长分成15cm和6cm两部分,而没有说明哪部分是15cm,哪部分是6cm;所以应该分两种情况进行讨论:第一种AB+AD=15cm,第二种AB+AD=6cm;分别求出其腰长及底边长,然后根据三角形三边关系定理将不合题意的解舍去.
点评:此题考查了等腰三角形的性质以及三角形的三边关系.此题难度不大,注意方程思想与分类讨论思想的应用是正确解答本题的关键.

 解:如图,根据题意得:AB=AC,AD=CD,
解:如图,根据题意得:AB=AC,AD=CD, ,
,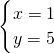 ,
, ,
, ,
,
