(1)解:(x+4)
2=5(x+4),
移项得:(x+4)
2-5(x+4)=0,
即(x+4)(x+4-5)=0,
∴x+4-5=0,x+4=0,
解方程得:x
1=1或x
2=-4,
(2)解:2x
2-10x=3,
x
2-5x=

,
x
2-5x+

=

+

,
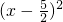
=
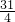
,
x-

=±
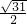
,
∴x
1=
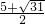
,x
2=
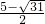
.
解:(3)
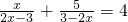
,
方程变为:

-
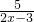
=4,
方程两边乘以2x-3得:x-5=4(2x-3),
解得:x=1,
检验:把x=1代入2x-3≠0,
∴x=1是原方程的解.
即原方程的解是x=1.
(4)解:
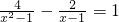
,
方程两边乘以(x+1)(x-1)得:
4-2(x+1)=(x+1)(x-1),
解方程得:x
1=-3,x
2=1,
检验:把x
1=-3,代入(x+1)(x-1)≠0,把x
2=1代入(x+1)(x-1)=0,
∴x=-3是方程的解,x=1不是方程的解,
∴原方程的解是x=-3.
分析:(1)移项后把方程的左边分解因式得到即(x+4)(x+4-5)=0,推出方程x+4-5=0,x+4=0,求出即可;
(2)把方程配方得到
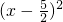
=
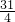
,开方后得到两个一元一次方程,求出方程的解即可;
(3)方程变为

-
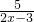
=4,方程两边乘以2x-3得到整式方程,求出方程的解检验即可;
(4)方程两边乘以(x+1)(x-1)得到方程4-2(x+1)=(x+1)(x-1),求出方程的解后检验即可.
点评:本题主要考查对解一元二次方程-因式分解法、配方法,解一元一次方程,分式方程,等式的性质等知识点的理解和掌握,能把一元二次方程转化成一元一次方程和把分式方程转化成整式方程是解此题的关键.

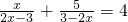
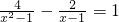 .
. ,
, =
= +
+ ,
,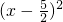 =
=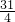 ,
, =±
=±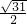 ,
,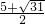 ,x2=
,x2=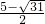 .
.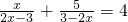 ,
, -
-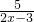 =4,
=4,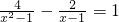 ,
,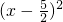 =
=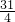 ,开方后得到两个一元一次方程,求出方程的解即可;
,开方后得到两个一元一次方程,求出方程的解即可; -
-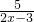 =4,方程两边乘以2x-3得到整式方程,求出方程的解检验即可;
=4,方程两边乘以2x-3得到整式方程,求出方程的解检验即可;

 阅读快车系列答案
阅读快车系列答案