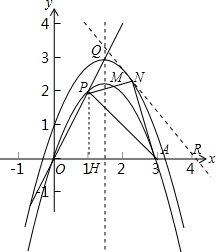
解:(1)过点P作PH⊥OA,垂足为点H.
∵点P在直线y=2x上,
∴设点P的坐标为(x,2x).
∵∠PAO=45°,PH⊥OA,
∴∠PAO=∠APH=45°.
∴PH=AH=2x.
∵点A的坐标为(3,0),
∴x+2x=3.
∴x=1.
∴点P的坐标为(1,2),
设所求的二次函数解析式为y=ax
2+bx+c(a≠0).
∵图象经过P(1,2)、O(0,0)、A(3,0)三点,
∴
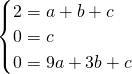
,
解得:

,
∴所求的二次函数解析式为y=-x
2+3x.
∴顶点M的坐标为(

,3),
故答案为:y=-x
2+3x;(

,3),
(2)根据题意,得点Q的坐标为(

,3),
∵S
△AQO=

×3×3=

,S
△APO=

×3×2=3,S
四边形AMPO=

×1×2+

×(2+

)×

+

×

×

=

,
∴S
△APM=

-3=

,S
△APQ=

-3=

,
∴△APM与△APQ的面积之比为

;
(3)设AP的解析式为:y=kx+b,N到AP的最大距离为k,
∵A(3,0),P(1,2)
∴
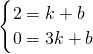
,
∴
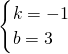
,
∴y=-x+3,
∴点N所在的直线NR的解析式为y=-x+3+k,
根据点Q(

,3)的坐标可知平移后的二次函数解析式为y=-(x-

)
2+3,
∴-(x-

)
2+3=-x+3+k,
因为只要唯一一个交点,所以△=0,
∴k=

,
∴x=2,y=

,
∴△APN的面积最大时,求点N的坐标是(2,

).
分析:(1)先根据题意设点P的坐标为(x,2x),又由∠PAO=45°,PH⊥OA,可得PH=AH=2x,又由点A的坐标为(3,0),即可求得x的值,则可求得点P的坐标,再利用待定系数法将点P,O,A的坐标代入解析式即可得到方程组,解方程组即可求得解析式,利用公式即可求出顶点的坐标;
(2)根据图形求得:△APO、△AQO与四边形AMPO的面积,即可求得△APM与△APQ的面积,则问题得解;
(3)因为AP的长度不变,N可以看做是直线AP延向上的方向平移和抛物线的唯一一个交点,设N到AP的最大距离为k,此时△APN的面积最大.
点评:本题主要考查了二次函数和一次函数解析式的确定、函数图象交点的求法以及三角形面积的求法等知识点.主要考查学生数形结合的数学思想方法.

 如图,A点坐标为(3,0),第一象限内的点P在直线y=2x上,且∠PAO=45°.
如图,A点坐标为(3,0),第一象限内的点P在直线y=2x上,且∠PAO=45°.
 ,
, ,
, ,3),
,3), ,3),
,3), ,3),
,3), ×3×3=
×3×3= ,S△APO=
,S△APO= ×3×2=3,S四边形AMPO=
×3×2=3,S四边形AMPO= ×1×2+
×1×2+ ×(2+
×(2+ )×
)× +
+ ×
× ×
× =
= ,
, -3=
-3= ,S△APQ=
,S△APQ= -3=
-3= ,
, ;
; ,
, ,
, ,3)的坐标可知平移后的二次函数解析式为y=-(x-
,3)的坐标可知平移后的二次函数解析式为y=-(x- )2+3,
)2+3, )2+3=-x+3+k,
)2+3=-x+3+k, ,
, ,
, ).
).

 名校课堂系列答案
名校课堂系列答案 (2012•西城区一模)已知:如图,A点坐标为(-
(2012•西城区一模)已知:如图,A点坐标为(-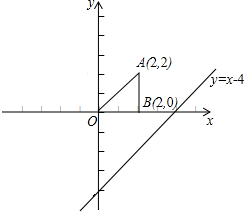 如图,A点坐标为(2,2),B点坐标为(2,0).
如图,A点坐标为(2,2),B点坐标为(2,0).