

分析 (1)欲证明BE是切线,只要证明∠OBE=90°即可.
(2)由△EBC∽△BAC,得到BC:AC=EC:BC,即BC2=CE•CA,由tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$,设,AC=4k,BC=3k,推出CE=$\frac{9}{4}$k,在Rt△ABC中,根据AB2=BC2+AC2,
列出方程求出k即可解决问题.
解答 (1)证明:如图连接OC.
∵CD是切线,
∴OC⊥CD,
∴∠COD=90°,
∵OC=OB,
∴∠OCB=∠OBC,∵∠DCB=∠DBC,
∴∠DCB+∠OCB=∠DBC+∠OBC=90°,
∴∠DBO=90°,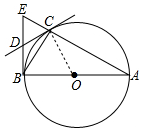
∴OB⊥EB,'
∴BE是⊙O的切线.
(2)解:∵AB是直径,
∴∠BCA=∠ECB=90°,
∵∠A+∠ABC=90°,∠EBC+∠ABC=90°,
∴∠EBC=∠A,
∴△EBC∽△BAC,
∴BC:AC=EC:BC,
∴BC2=CE•CA,
∵tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{3}$,设,AC=4k,BC=3k,
∴CE=$\frac{9}{4}$k,
在Rt△ABC中,∵AB2=BC2+AC2,
∴4=25k2,
∵k>0,
∴k=$\frac{2}{5}$,
∴EC=$\frac{9}{4}$×$\frac{2}{5}$=$\frac{9}{10}$.
点评 本题考查切线的判定、直径的性质、等腰三角形的性质、相似三角形的判定和性质、锐角三角函数、勾股定理等知识,解题的关键是灵活运用所学知识,学会利用参数解决问题,属于中考常考题型.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,抛物线y=ax2-8ax(a>0)与x轴交于O,A两点,它的顶点为P,经过O,A两点的圆⊙M与y轴交于点B,抛物线的对称轴与⊙M交于点C,连接AB,BP,当CD:DM:CP=2:3:4时,tan∠ABP的值是$\frac{9}{13}$.
如图,抛物线y=ax2-8ax(a>0)与x轴交于O,A两点,它的顶点为P,经过O,A两点的圆⊙M与y轴交于点B,抛物线的对称轴与⊙M交于点C,连接AB,BP,当CD:DM:CP=2:3:4时,tan∠ABP的值是$\frac{9}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,已知点A(-1,0),B(3,2),将线段AB绕点A旋转90°,得到线段AB′,则点B′的坐标是(-3,4)或(1,-4).
如图,在平面直角坐标系中,已知点A(-1,0),B(3,2),将线段AB绕点A旋转90°,得到线段AB′,则点B′的坐标是(-3,4)或(1,-4).查看答案和解析>>
科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列运算正确的是( ).
A. a3+a4=a7 B. 2a3•a4=2a7 C. (2a4)3=8a7 D. a8÷a2=a4
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:判断题
如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.

查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
三条线段a=5,b=3,c的值为整数,由a、b、c为边可组成三角形( )
A. 1个 B. 3个 C. 5个 D. 无数个
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省佛山市顺德区八年级3月月考数学试卷(解析版) 题型:填空题
如图,直线y=x+b与直线y=kx+6交于点P(3,5),则关于x的不等式x+b>kx+6的解集是_____________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com