
 如图,在平面直角坐标系中,已知点A(-1,0),B(3,2),将线段AB绕点A旋转90°,得到线段AB′,则点B′的坐标是(-3,4)或(1,-4).
如图,在平面直角坐标系中,已知点A(-1,0),B(3,2),将线段AB绕点A旋转90°,得到线段AB′,则点B′的坐标是(-3,4)或(1,-4). 分析 由于题目没有说明顺时针旋转还是逆时针旋转,故需要分情况讨论.
解答 解:当AB绕点A逆时针旋转90°,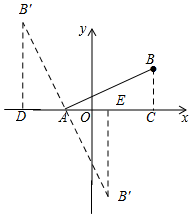
此时过点B′作B′D⊥x轴于点D,
∵∠BAC+∠B′AD=90°,
∠DB′A+∠B′AD=90°,
在△B′DA与△ACB中,
$\left\{\begin{array}{l}{∠B′DA=∠ACB}\\{∠DB′A=∠BAC}\\{AB′=AB}\end{array}\right.$
∴△B′DA≌△ACB(AAS),
∴AD=BC,B′D=AC
∵A(-1,0),B(3,2),
∴BC=2,AC=4,
∴B′(-3,4),
当AB绕点A顺时针旋转90°时,
过点B′作B′E⊥x轴于点E,
同理可求得:B′(1,-4)
故答案为:(-3,4)或(1,-4)
点评 本题考查考查旋转的性质,涉及旋转的三要素,全等三角形的性质与判定.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:解答题
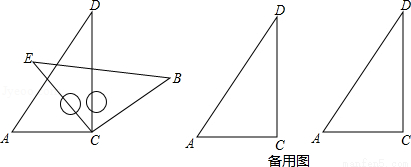
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年广东省佛山市顺德区八年级3月月考数学试卷(解析版) 题型:解答题
已知:如图,在△ABC中,AB=AC,点D是BC边上的中点,DE、DF分别垂直AB、AC于点E和F.求证:DE=DF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com