Question

14．如图，在平面直角坐标系中，直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x²+bx+c交于A、B两点，点A在x轴上，点B的横坐标为-8．
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线交x轴于点C，交直线AB于点D，作PE⊥AB于点E．
①已知△PDE的周长为l2，求点P的横坐标；
②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形APFG的大小、位置也随之改变．当顶点F恰好落在抛物线的对称轴上时，直接写出对应的点P的坐标．

Answer 1

分析 （1）利用直线解析式求出点A、B的坐标，再利用待定系数法求二次函数解析式解答；
（2）①利用直线解析式和抛物线解析式表示出PD，再利用同角的余角相等求出∠DPE=∠BAO，根据直线k值求出∠BAO的正弦和余弦值，然后表示出PE、DE，再根据三角形的周长公式列式整理即可得解，再根据二次函数的最值问题解答；
②点G在y轴上时，过点P作PH⊥x轴于H，根据正方形的性质可得AP=AG，∠PAG=90°，再求出∠PAH=∠AGO，然后利用“角角边”证明△APH和△GAO全等，根据全等三角形对应边相等可得PH=AO=2，然后利用二次函数解析式求解即可；

解答 解：（1）令y=0，则 $\frac{3}{4}$x-$\frac{3}{2}$=0，解得x=2，
x=-8时，y=$\frac{3}{4}$×（-8）-$\frac{3}{2}$=-$\frac{15}{2}$，
∴点A（2，0），B（-8，-$\frac{15}{2}$），
把点A、B代入抛物线得，$\left\{\begin{array}{l}{-1+2b+c=0}\\{-16-8b+c=-\frac{15}{2}}\end{array}\right.$，$\left\{\begin{array}{l}{b=-\frac{3}{4}}\\{c=\frac{5}{2}}\end{array}\right.$
解得，
所以，该抛物线的解析式y=-$\frac{1}{4}$x²-$\frac{3}{4}$x+$\frac{5}{2}$；

（2）①∵点P在抛物线上，点D在直线上，
∴PD=-$\frac{1}{4}$x²-$\frac{3}{4}$x+$\frac{5}{2}$-（ $\frac{4}{3}$x-$\frac{3}{2}$）=-$\frac{1}{4}$x²-$\frac{3}{2}$x+4，
∵PE⊥AB，
∴∠DPE+∠PDE=90°，
又∵PD⊥x轴，
∴∠BAO+∠PDE=90°，
∴∠DPE=∠BAO，
∵直线解析式k=$\frac{3}{4}$，
∴sin∠BAO=$\frac{3}{5}$，cos∠BAO=$\frac{4}{5}$，
∴PE=PDcos∠DPE=$\frac{4}{5}$PD，
DE=PDsin∠DPE=$\frac{3}{5}$PD，
∴△PDE的周长为l=PD+$\frac{3}{5}$PD+$\frac{4}{5}$PD=$\frac{12}{5}$PD=$\frac{12}{5}$（-$\frac{1}{4}$x²-$\frac{3}{2}$x+4）=-$\frac{3}{5}$x²-$\frac{18}{5}$x+$\frac{48}{5}$，
即l=-$\frac{3}{5}$x²-$\frac{18}{5}$x+$\frac{48}{5}$；
∵l=-$\frac{3}{5}$（x²+6x+9）+15，
∴当x=-3时，最大值为15；

②当点G在y轴上时，过点P作PH⊥x轴于H，如图1中，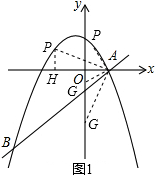

∵点A（2，0），
∴AO=2，
∵在正方形APFG中，AP=AG，∠PAG=90°，
∵∠PAH+∠OAG=90°，∠AGO+∠OAG=90°，
∴∠PAH=∠AGO，
在△APH和△GAO中，
$\left\{\begin{array}{l}{∠PAH=∠AGO}\\{∠AHP=∠GOA=90°}\\{AP=AG}\end{array}\right.$，
∴△APH≌△GAO（AAS），
∴PH=AO=2，
∴点P的纵坐标为2，
∴-$\frac{1}{4}$x²-$\frac{3}{4}$x+$\frac{5}{2}$=2，
整理得，x²+3x-2=0，
解得x=$\frac{-3±\sqrt{17}}{2}$，
∴点P₁（ $\frac{-2+\sqrt{17}}{2}$，2），P₂（ $\frac{-3-\sqrt{17}}{2}$，2）；

点评 此题主要考查了二次函数的综合应用，全等三角形的判定与性质以及待定系数法求二次函数解析式，锐角三角函数的应用等知识，解题的关键是学会构建二次函数，利用二次函数的性质解决实际问题，学会添加常用辅助线构造直角三角形解决问题．属于中考压轴题．