
 如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为(3$\sqrt{2}$-1)cm.
如图,正方形ABCD中,AB=3cm,以B为圆心,1cm长为半径画⊙B,点P在⊙B上移动,连接AP,并将AP绕点A逆时针旋转90°至AP′,连接BP′.在点P移动的过程中,BP′长度的最小值为(3$\sqrt{2}$-1)cm. 分析 通过画图发现,点P′的运动路线为以D为圆心,以1为半径的圆,可知:当P′在对角线BD上时,BP′最小,先证明△PAB≌△P′AD,则P′D=PB=1,再利用勾股定理求对角线BD的长,则得出BP′的长.
解答 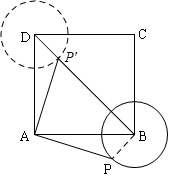 解:如图,当P′在对角线BD上时,BP′最小,
解:如图,当P′在对角线BD上时,BP′最小,
连接BP,
由旋转得:AP=AP′,∠PAP′=90°,
∴∠PAB+∠BAP′=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAP′+∠DAP′=90°,
∴∠PAB=∠DAP′,
∴△PAB≌△P′AD,
∴P′D=PB=1,
在Rt△ABD中,∵AB=AD=3,
由勾股定理得:BD=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴BP′=BD-P′D=3$\sqrt{2}$-1,
即BP′长度的最小值为(3$\sqrt{2}$-1)cm.
故答案为:(3$\sqrt{2}$-1).
点评 本题考查了正方形的性质、旋转的性质和最小值问题,寻找点P′的运动轨迹是本题的关键,通过证明两三角形全等求出BP′长度的最小值最小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题

| A. | 90 | B. | 91 | C. | 140 | D. | 141 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:解答题
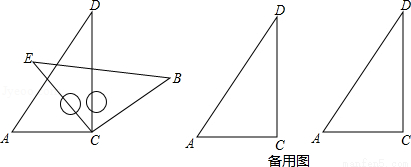
将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com