
| A. | m>-$\frac{5}{3}$ | B. | m≤$\frac{1}{2}$ | C. | m<-$\frac{5}{3}$ | D. | -$\frac{5}{3}$<m≤$\frac{1}{2}$ |
分析 先利用判别式的意义得到m≤$\frac{1}{2}$,再根据根与系数的关系,由x1x2>x1+x2-4得到$\frac{3m-1}{2}$>1-4,此时解得m>-$\frac{5}{3}$,然后写出满足条件的m的取值范围.
解答 解:根据题意得△=(-2)2-4×2×(3m-1)≥0,解得m≤$\frac{1}{2}$,
∵x1+x2=1,x1x2=$\frac{3m-1}{2}$,
而x1x2>x1+x2-4,
∴$\frac{3m-1}{2}$>1-4,解得m>-$\frac{5}{3}$,
∴m的取值范围为-$\frac{5}{3}$<m≤$\frac{1}{2}$.
故选D.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.


科目:初中数学 来源:2016-2017学年四川省眉山市第九年级下学期第一次月考数学试卷(解析版) 题型:单选题
“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A.  B.
B. 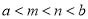
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是h=n+6.
小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是h=n+6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$-$\frac{1}{3}$ | B. | -$\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$-$\frac{1}{3}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.
如图,在平面直角坐标系中,直线y=$\frac{3}{4}$x-$\frac{3}{2}$与抛物线y=-$\frac{1}{4}$x2+bx+c交于A、B两点,点A在x轴上,点B的横坐标为-8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
如图,对于图中标记的各角,下列条件能够推理得到a∥b的是( )

A. ∠1=∠4 B. ∠2=∠4 C. ∠3+∠2=∠4 D. ∠2+∠3+∠4=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com