
【题目】如图,已知![]() 为直角三角形,
为直角三角形,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() ,线段
,线段![]() 与
与![]() 轴相交于点
轴相交于点![]() ,以
,以![]() 为顶点的抛物线过点
为顶点的抛物线过点![]() .
.
(1)求点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(2)求抛物线的解析式;
(3)设点![]() 为抛物线上点
为抛物线上点![]() 至点
至点![]() 之间的一动点,连接
之间的一动点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,试证明:
,试证明:![]() 为定值.
为定值.
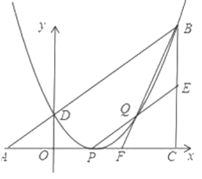
【答案】(1)点![]() 的坐标是
的坐标是![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)AO=AC-OC=m-3,用线段的长度表示点A的坐标;
(2)∵△ABC是等腰直角三角形,∴△AOD也是等腰直角三角形,∴OD=OA,∴D(0,m-3),又P(1,0)为抛物线顶点,可设顶点式,求解析式;
(3)设Q(x,x2-2x+1),过Q点分别作x轴,y轴的垂线,运用相似比求出FC、EC的长,而AC=m,代入即可.
(1)解:由![]() 可知
可知![]() ,
,![]() ,又
,又![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ;
;
(2)解:∵![]() ,
,
∴![]() ,则点
,则点![]() 的坐标是
的坐标是![]() ,
,
又抛物线顶点为![]() ,且过点
,且过点![]() ,
,
所以可设抛物线的解析式为:![]() ,
,
得![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为![]() ;
;
(3)证明:过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
设点![]() 的坐标是
的坐标是![]() ,
,
则![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
得![]() ,
,
∵![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
得![]() ,
,
又∵![]() ,
,
∴![]() ,
,
即![]() 为定值8.
为定值8.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的布袋,甲袋中装有3个完全相同的小球,分别标有数字0,1,2;乙袋中装有3个完全相同的小球,分别标有数字﹣1,﹣2,0;现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M坐标为(x,y).
(1)用树状图或列表法列举点M所有可能的坐标;
(2)求点M(x,y)在函数y=-x+1的图象上的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
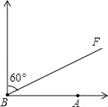
【题目】如图,A城气象台测得台风中心在A城的正西方300千米处,以每小时10![]() 千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
千米的速度向北偏东60°的BF方向移动,距台风中心200千米的范围内是受这次台风影响的区域.
(1)问A城是否会受到这次台风的影响?为什么?
(2)若A城受到这次台风的影响,那么A城遭受这次台风影响的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
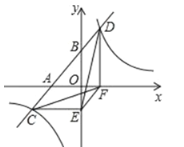
【题目】如图,一次函数 ![]() 与
与![]() 轴,
轴,![]() 轴交于
轴交于![]() 两点,与反比例函数
两点,与反比例函数![]() 相交于
相交于![]() 两点,分别过
两点,分别过![]() 两点作
两点作![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,连接
,连接![]() ,有下列四个结论:①
,有下列四个结论:①![]() 与
与![]() 的面积相等;②
的面积相等;②![]() ∽
∽![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论个数是( )
,其中正确的结论个数是( )
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校2017年在某商场购买甲、乙两种不同足球,购买甲种足球共花费2000元,购买乙种足球共花费1400元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元;
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)2018年这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2910元,那么这所学校最多可购买多少个乙种足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村在推进美丽乡村活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调査.获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.
(1)红色地砖与蓝色地砖的单价各多少元?
(2)经过测算,需要购置地砖12000块,其中蓝色地砖的数量不少于红色地砖的一半,并且不超过6000块,如何购买付款最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com