
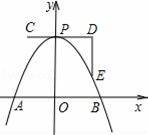
如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )

A.1 B.2 C.3 D.4
B【考点】二次函数综合题.
【专题】压轴题;动点型.
【分析】抛物线在平移过程中形状没有发生变化,因此函数解析式的二次项系数在平移前后不会改变.首先,当点B横坐标取最小值时,函数的顶点在C点,根据待定系数法可确定抛物线的解析式;而点A横坐标取最大值时,抛物线的顶点应移动到E点,结合前面求出的二次项系数以及E点坐标可确定此时抛物线的解析式,进一步能求出此时点A的坐标,即点A的横坐标最大值.
【解答】解:由图知:当点B的横坐标为1时,抛物线顶点取C(﹣1,4),设该抛物线的解析式为:y=a(x+1)2+4,代入点B坐标,得:
0=a(1+1)2+4,a=﹣1,
即:B点横坐标取最小值时,抛物线的解析式为:y=﹣(x+1)2+4.
当A点横坐标取最大值时,抛物线顶点应取E(3,1),则此时抛物线的解析式:y=﹣(x﹣3)2+1=﹣x2+6x﹣8=﹣(x﹣2)(x﹣4),即与x轴的交点为(2,0)或(4,0)(舍去),
∴点A的横坐标的最大值为2.
故选B.


【点评】考查了二次函数综合题,解答该题的关键在于读透题意,要注意的是抛物线在平移过程中形状并没有发生变化,改变的是顶点坐标.注意抛物线顶点所处的C、E两个关键位置,前者能确定函数解析式、后者能得到要求的结果.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线.
(2)当OA=3,AE=4时,求BC的长度.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com