
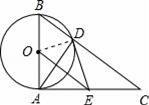
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
(1)求证:ED是⊙O的切线.
(2)当OA=3,AE=4时,求BC的长度.


【考点】切线的判定;垂径定理.
【专题】几何综合题.
【分析】(1)如图,连接OD.通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得结论;
(2)利用圆周角定理和垂径定理推知OE∥BC,所以根据平行线分线段成比例求得BC的长度即可.
【解答】(1)证明:如图,连接OD.
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
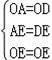
 ,
,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)解:如图,在△OAE中,∠OAE=90°,OA=3,AE=4,
∴由勾股定理易求OE=5.
∵AB是直径,
∴∠ADB=90°,即AD⊥BC.
又∵由(1)知,△AOE≌△DOE,
∴∠AEO=∠DEO,
又∵AE=DE,
∴OE⊥AD,
∴OE∥BC,
∴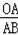
 =
=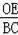
 =
=
 .
.
BC=2OE=10,即BC的长度是10.

【点评】本题考查了切线的判定与性质.解答(2)题时,也可以根据三角形中位线定理来求线段BC的长度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
如图,AC是矩形ABCD的对角线,AB=2,BC=2
 ,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF= .
,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF= .


查看答案和解析>>
科目:初中数学 来源: 题型:
今年要实现大病保险全覆盖,中央财政安排城乡医疗救助补助资金160亿元,160亿元这一数据用科学记数法表示为( )
A.16×109元 B.1.6×1010元 C.0.16×1011元 D.1.6×109元
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,连接BC,若∠ABC=45°,则下列结论正确的是( )


A.AC>AB B.AC=AB C.AC<AB D.AC=
 BC
BC
查看答案和解析>>
科目:初中数学 来源: 题型:
今年1至4月份,我省旅游业一直保持良好的发展势头,旅游收入累计达5 163 000 000元,用科学记数法表示是( )
A.5.163×106元 B.5.163×108元 C.5.163×109元 D.5.163×1010元
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C﹣D﹣E上移动,若点C、D、E的坐标分别为(﹣1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
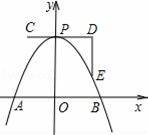

A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com