
科目:初中数学 来源:不详 题型:解答题
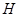 点,并测得HB=6m.
点,并测得HB=6m.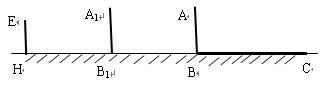
 在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;
在图中画出形成影子的光线,并确定路灯灯泡所在的位置G;查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
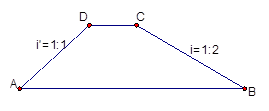
 .容易知道一个角的大小与这个角的正对值也是相互
.容易知道一个角的大小与这个角的正对值也是相互 唯一确定的.根据上述角的正对定义,解下列问题:
唯一确定的.根据上述角的正对定义,解下列问题:
 ,试求sad A的值
,试求sad A的值
|
 | |||
 | |||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com