
分析 (1)设每个16G和32G U盘的进价分别是x元、y元,根据购进16G U盘3个和32G U盘4个共需370元;购进16G U盘4个和32G U盘3个共需330元,列出相应的方程组,从而可以解答本题;
(2)根据题意可以得到利润与16G U盘个数的函数解析式,由16G U盘的数量不少于32G U盘数量的4倍,可以得到16G U盘的取值范围,从而可以求得获利最大的进货方案,以及最大利润.
解答 解:(1)设每个16G和32G U盘的进价分别是x元、y元,
由题意,得$\left\{\begin{array}{l}{3x+4y=370}\\{4x+3y=330}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=30}\\{y=70}\end{array}\right.$,
答:每个16G和32U盘的进价分别是30元、70元;
(2)设购买16G U盘a个,获利为w元,
w=(40-30)a+(90-70)(100-a)=-10a+2000,
∵a≥4(100-a),
解得,a≥80,
∴当a=80时,w取得最大值,此时w=1200,
即获利最大的进货方案是购买16G U盘80个,32G U盘20个,最大利润是1200元.
点评 本题考查一次函数的应用、二元一次方程组的应用、一元一次不等式的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质和不等式的性质解答问题.


科目:初中数学 来源: 题型:解答题
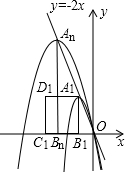 我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
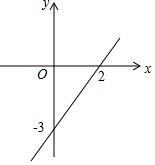 已知一次函数的图象如图所示.
已知一次函数的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
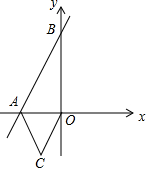 如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )
如图,直线y=2x+4与x轴、y轴分别交于A、B两点,以OA为边在x轴的下方作等边三角形OAC,将点C向上平移m个单位长度,使其对应点C′恰好落在直线AB上,则m=( )| A. | 2-$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 4-$\sqrt{3}$ | D. | 4$+\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
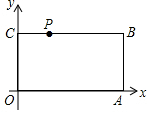 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA中点,点P在边BC上运动,当△ODP是等腰三角形时,点P的坐标为(2,4)或(2.5,4)或(3,4)或(8,4).
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA中点,点P在边BC上运动,当△ODP是等腰三角形时,点P的坐标为(2,4)或(2.5,4)或(3,4)或(8,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
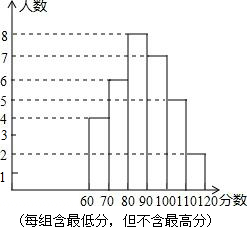 某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数直方图,如图所示.
某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了频数直方图,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品牌 价格 | A品牌 | B品牌 |
| 进价(元/部) | 3800 | 3000 |
| 售价(元/部) | 4500 | 3500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com