
| A. | 1<m<7 | B. | 3<m<4 | C. | m>1 | D. | m<4 |
分析 直线y=-x-3向上平移m个单位后可得:y=-x-3+m,求出直线y=-x-3+m与直线y=2x+4的交点,再由此点在第二象限可得出m的取值范围.
解答 解:直线y=x-3向上平移m个单位后可得:y=-x-3+m,
联立两直线解析式得:$\left\{\begin{array}{l}{y=-x-3+m}\\{y=2x+4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{1}{3}(m-7)}\\{y=\frac{2}{3}(m-7)+4}\end{array}\right.$,
即交点坐标为($\frac{1}{3}$(m-7),$\frac{2}{3}$(m-7)+4),
∵交点在第二象限,
∴$\left\{\begin{array}{l}{\frac{1}{3}(m-7)<0}\\{\frac{2}{3}(m-7)+4>0}\end{array}\right.$,
解得:1<m<7.
故选A.
点评 本题考查了一次函数图象与几何变换、两直线的交点坐标,注意第二象限的点的横坐标小于0、纵坐标大于0.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:选择题
 如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.
如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.| A. | 3 | B. | 6 | C. | 8 | D. | $\sqrt{17}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴
如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴查看答案和解析>>
科目:初中数学 来源: 题型:解答题
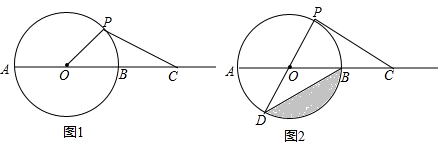
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
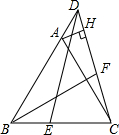 如图,已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E.∠ABC的平分线BF,交CD于点F,过点A作AH⊥CD于H.当∠EDC=30°,CF=$\frac{4}{3}$,则DH=$\frac{2}{3}$.
如图,已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E.∠ABC的平分线BF,交CD于点F,过点A作AH⊥CD于H.当∠EDC=30°,CF=$\frac{4}{3}$,则DH=$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (3,-2) | C. | (-2,3) | D. | (3,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com