练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．如图，将矩形ABCD密铺在长为4cm．宽为2cm的矩形纸片右侧，若组成的新矩形与原矩形（图中阴影部分）相似，则AB=（　　）cm．
    A．3B．6C．8D．$\sqrt{17}$-1

    分析 根据相似三角形的性质列出比例式，计算即可．

    解答 解：∵新矩形与原矩形相似，
    ∴$\frac{2}{4}$=$\frac{4}{2+AB}$，
    解得AB=6．
    故选：B．

    点评 本题考查的是相似多边形的性质，掌握相似多边形的对应角相等、对应边的比相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．下列方程中是一元一次方程的是（　　）
    A．5=abB．2+5=7C．$\frac{x}{2}$+1=x+3D．3x+5y=8

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

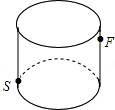    2．如图所示，圆柱形玻璃容器，高18cm，底面周长为60cm，在外侧距下底1cm，点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一苍蝇，试求急于捕获苍蝇充饥的蜘蛛，所走的最短路线的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．（1）已知ax=5，ax+y=25，求ax+ay的值；
    （2）已知10α=5，10β=6，求102α-2β的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

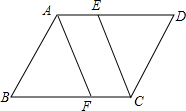    6．如图所示，平行四边形ABCD中，点E、F分别为边AD与CB的三等分点，试证明：
    （1）四边形AFCE为平行四边形；
    （2）△ABF≌△CDE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

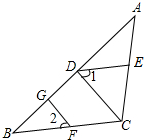    16．如图，已知FG⊥AB，CD⊥AB，垂足分别为G，D，∠1=∠2，
    求证：∠CED+∠ACB=180°，
    请你将小明的证明过程补充完整．
    证明：∵FG⊥AB，CD⊥AB，垂足分别为G，D（已知）
    ∴∠FGB=∠CDB=90°（垂直定义）．
    ∴GF∥CD（同位角相等，两直线平行）
    ∵GF∥CD（已证）
    ∴∠2=∠BCD两直线平行，同位角相等）
    又∵∠1=∠2（已知）
    ∴∠1=∠BCD（等量代换）
    ∴DE∥BC（内错角相等，两直线平行）
    ∴∠CED+∠ACB=180°（两直线平行，同旁内角互补）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知，一条抛物线的顶点为E（-1，4），且过点A（-3，0），与y轴交于点C，点D是这条抛物线上一点，它的横坐标为m，且-3＜m＜-1，过点D作DK⊥x轴，垂足为K，DK分别交线段AE、AC于点G、H．
    （1）求这条抛物线的解析式；
    （2）求证：GH=HK；
    （3）当△CGH是等腰三角形时，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．把直线y=-x-3向上平移m个单位后，与直线y=2x+4的交点在第二象限，则m的取值范围是（　　）
    A．1＜m＜7B．3＜m＜4C．m＞1D．m＜4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．认真阅读以下材料，并解答问题：
    材料：（1）配方：利用完全平方公式，把二次三项式写成（a-k）2+h的形式．
    例：x2-2x=x2-2•1•x+12-12=（x-1）2-1
    （2）利用配方法解方程ax2+bx+c=0（a≠0）
    问题：（1）把多项式直接写成（a-k）2+h的形式：x2-6x-3=（x-3）2-12
    （2）用配方法解方程：x2+6x+8=0．

    查看答案和解析>>

    同步练习册答案