
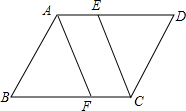
 如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明:
如图所示,平行四边形ABCD中,点E、F分别为边AD与CB的三等分点,试证明:分析 (1)直接利用平行四边形的对边平行且相等,进而得出AE$\stackrel{∥}{=}$FC,即可得出答案;
(2)利用平行四边形的性质得出AB=DC,AD=BC,∠B=∠D,进而结合全等三角形的判定方法得出答案.
解答 证明:(1)∵四边形ABCD是平行四边形,
∴AD$\stackrel{∥}{=}$BC,
∵点E、F分别为边AD与CB的三等分点,
∴AE=$\frac{1}{3}$AD,FC=$\frac{1}{3}$BC,
∴AE$\stackrel{∥}{=}$FC,
∴四边形AFCE为平行四边形;
(2)∵四边形ABCD是平行四边形,
∴AB=DC,AD=BC,∠B=∠D,
∵点E、F分别为边AD与CB的三等分点,
∴DE=$\frac{2}{3}$AD,FB=$\frac{2}{3}$BC,
∴BF=DE,
在△ABF和△CDE中
∵$\left\{\begin{array}{l}{AB=DC}\\{∠B=∠D}\\{BF=DE}\end{array}\right.$,
∴△ABF≌△CDE.
点评 此题主要考查了平行四边形的判定与性质以及全等三角形的判定与性质,正确应用平行四边形的性质是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.
如图,将矩形ABCD密铺在长为4cm.宽为2cm的矩形纸片右侧,若组成的新矩形与原矩形(图中阴影部分)相似,则AB=( )cm.| A. | 3 | B. | 6 | C. | 8 | D. | $\sqrt{17}$-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第6块.
如图,一块铁片边缘是由抛物线和线段AB组成,测得AB=20cm,抛物线的顶点到AB边的距离为25cm.现要沿AB边向上依次截取宽度均为4cm的矩形铁皮,从下往上依次是第一块,第二块…如图所示.已知截得的铁皮中有一块是正方形,则这块正方形铁皮是第6块.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com