
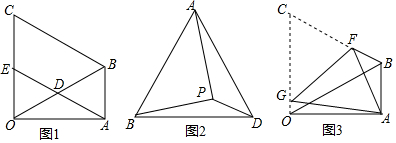
分析 (1)首先根据直角三角形中斜边上的中线等于斜边的一半可得DO=DA,再根据等边对等角可得∠DAO=∠DOA=30°,进而算出∠AEO=60°,再证明BC∥AE,CO∥AB,进而证出四边形ABCE是平行四边形;
(2)根据△ABD是等边三角形,作辅助线,如图2,得到△PCP′是等边三角形,△APP′是直角三角形,由勾股定理得:PP′的长,由此可知:∠PAP′=30°,则∠APP′=60°,根据周角计算∠APB=90°,最后利用勾股定理求AB的长;
(3)设OG=x,由折叠可得:AG=GC=2AB-x,再利用三角函数可计算出AO,再利用勾股定理表示出线段OG与AB的数量关系,得:AB=4x,OB=8x,作辅助线,构建直角三角形ABH,同理设BF=a,根据勾股定理列方程得出a=$\frac{12}{5}x$,最后计算OG:BF的比值即可.
解答 证明:(1)∵Rt△OAB中,D为OB的中点,
∴DO=DA,
∴∠EAO=∠AOB=30°,
∵△OBC为等边三角形,
∵∠COB=60°,
又∵∠AOB=30°,
∴∠EOA=90°,
∴∠AEO=180°-∠EOA-∠EAO=180°-90°-30°=60°,
∴∠AEO=∠C,
∴BC∥AE,
∵∠BAO=∠COA=90°,
∴CO∥AB,
∴四边形ABCE是平行四边形;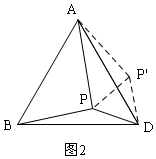
(2)由(1)得:△ABD是等边三角形,
如图2,将△BPD绕点D顺时针旋转60°得到△ADP′,连接PP′,
∴∠PDP′=∠ADB=60°,PD=P′D,∠AP′D=∠BPD=150°,
∴△PDP′是等边三角形,
∴∠PP′D=60°,
∴∠AP′P=150°-60°=90°,
在Rt△APP′中,由勾股定理得:PP′=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∴∠PAP′=30°,
∴∠APP′=60°,
∴∠APB=360°-150°-60°-60°=90°,
在Rt△APB中,由勾股定理得:AB=$\sqrt{{4}^{2}+(2\sqrt{3})^{2}}$=$\sqrt{28}$=2$\sqrt{7}$,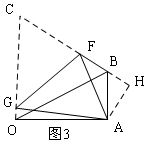
∴△ABD的边长为2$\sqrt{7}$;.
(3)如图3,在Rt△ABO中,
∵∠OAB=90°,∠AOB=30°,
∴BO=2AB,OA=$\sqrt{O{B}^{2}-A{B}^{2}}$=$\sqrt{3}$AB,
设OG=x,由折叠可得:AG=GC=2AB-x,
在Rt△OAG中,OG2+OA2=AG2,
x2+($\sqrt{3}$AB)2=(2AB-x)2,
解得:x=$\frac{1}{4}$AB,
即OG=$\frac{1}{4}$AB,
∴AB=4x,OB=8x,
过A作AH⊥BC,交CB的延长线于H,
∵∠CBO=∠OBA=60°,
∴∠ABH=60°,
Rt△ABH中,∠BAH=30°,
∴BH=$\frac{1}{2}$AB=2x,AH=2$\sqrt{3}$x,
设BF=a,则AF=FC=8x-a,
在Rt△AFH中,由勾股定理得:AF2=FH2+AH2,
$(8x-a)^{2}=(a+2x)^{2}+(2\sqrt{3}x)^{2}$,
a=$\frac{12}{5}$x,
∴$\frac{OG}{BF}$=$\frac{x}{\frac{12}{5}x}$=$\frac{5}{12}$,
故答案为:$\frac{5}{12}$.
点评 此题是四边形的综合题,主要考查了平行四边形的判定与性质,以及勾股定理的应用,图形的翻折变换,关键是掌握平行四边形的判定定理.第2问中的旋转辅助线是解题的关键,第3问分别设OG和BF为未知数,都与AB的联系,根据勾股定理列方程解决问题.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
| 运输工具 | 途中平均速度(千米/时) | 运费(元/千米) | 装卸费(元) |
| 汽车 | 50 | 20 | 900 |
| 火车 | 100 | 15 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
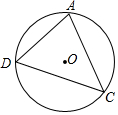 如图,△ADC内接于⊙O.
如图,△ADC内接于⊙O.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | △ABC是直角三角形 | B. | △ABC是等腰三角形 | ||
| C. | △ABC是等腰直角三角形 | D. | △ABC是锐角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com