
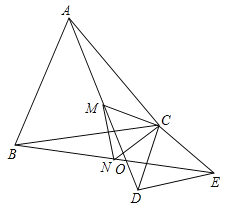
【题目】已知:如图,![]() 、
、![]() 都是等腰三角形,且
都是等腰三角形,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.以下4个结论:①
的中点.以下4个结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④连
是等边三角形;④连![]() ,则
,则![]() 平分
平分![]() 以上四个结论中正确的是:______.(把所有正确结论的序号都填上)
以上四个结论中正确的是:______.(把所有正确结论的序号都填上)
【答案】①②④
【解析】
①根据全等三角形的判定定理得到△ACD≌△BCE(SAS),由全等三角形的性质得到AD=BE;故①正确;
②设CD与BE交于F,根据全等三角形的性质得到∠ADC=∠BEC,得到∠DOE=∠DCE=α,根据平角的定义得到∠BOD=180°∠DOE=180°α,故②正确;
③根据全等三角形的性质得到∠CAD=∠CBE,AD=BE,AC=BC根据线段的中点的定义得到AM=BN,根据全等三角形的性质得到CM=CN,∠ACM=∠BCN,得到∠MCN=α,推出△MNC不一定是等边三角形,故③不符合题意;
④过C作CG⊥BE于G,CH⊥AD于H,根据全等三角形的性质得到CH=CG,根据角平分线的判定定理即可得到OC平分∠AOE,故④正确.
解:①∵CA=CB,CD=CE,∠ACB=∠DCE=α,
∴∠ACB+∠BCD=∠DCE+∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中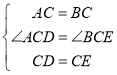 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE;故①正确;
②设CD与BE交于F,
∵△ACD≌△BCE,
∴∠ADC=∠BEC,
∵∠CFE=∠DFO,
∴∠DOE=∠DCE=α,
∴∠BOD=180°∠DOE=180°α,故②正确;
③∵△ACD≌△BCE,
∴∠CAD=∠CBE,AD=BE,AC=BC
又∵点M、N分别是线段AD、BE的中点,
∴AM= ![]() AD,BN=
AD,BN= ![]() BE,
BE,
∴AM=BN,
在△ACM和△BCN中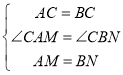 ,
,
∴△ACM≌△BCN(SAS),
∴CM=CN,∠ACM=∠BCN,
又∠ACB=α,
∴∠ACM+∠MCB=α,
∴∠BCN+∠MCB=α,
∴∠MCN=α,
∴△MNC不一定是等边三角形,故③不符合题意;
④如图,
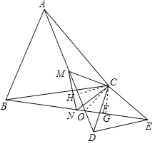
过C作CG⊥BE于G,CH⊥AD于H,
∴∠CHD=∠ECG=90°,∵∠CEG=∠CDH,CE=CD,
∴△CGE≌△CHD(AAS),
∴CH=CG,
∴OC平分∠AOE,故④正确,
故答案为①②④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】数学兴趣小组在“用面积验证平方差公式”时,经历了如下的探究过程;
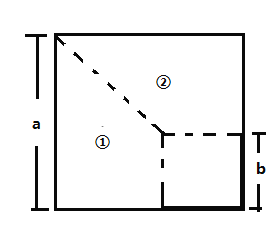
(1)小明的想法是:将边长为![]() 的正方形右下角剪掉一个边长为
的正方形右下角剪掉一个边长为![]() 的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,并用两种方式表示这两部分面积的和,请你按照小明的想法验证平方差公式.
的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,并用两种方式表示这两部分面积的和,请你按照小明的想法验证平方差公式.
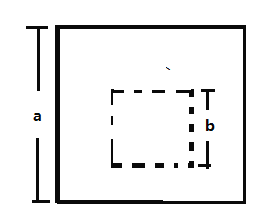
(2)小白的想法是:在边长为![]() 的正方形内部任意位置剪掉一个边长为
的正方形内部任意位置剪掉一个边长为![]() 的正方形(如图2),再将剩下部分进行适当分割,并将分割得到的几部分面积和用两种方式表示出来,请你按照小白的想法在图中用虚线画出分割线,并验证平方差公式.
的正方形(如图2),再将剩下部分进行适当分割,并将分割得到的几部分面积和用两种方式表示出来,请你按照小白的想法在图中用虚线画出分割线,并验证平方差公式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂需要在规定时间内生产1000个某种零件,该工厂按一定速度加工6天后,发现按此速度加工下去会延期4天完工,于是又抽调了一批工人投入这种零件的生产,使工作效率提高了![]() ,结果如期完成生产任务.
,结果如期完成生产任务.
(1)求该工厂前6天每天生产多少个这种零件;
(2)求规定时间是多少天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进甲、乙两种商品.已知甲商品每件进价15元,售价20元;乙商品每件进价35元,售价45元.
(1)若该商店同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)若该商店准备用不超过3100元购进甲、乙两种商品共100件,且这两种商品全部售出后获利不少于890元,问应该怎样进货,才能使总利润最大,最大利润是多少?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
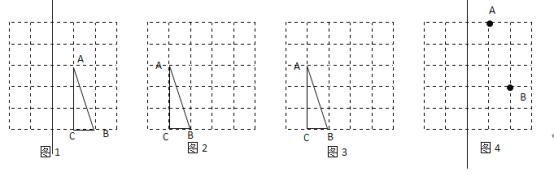
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点,
的小正方形构成的网格,每个小正方形的顶点叫做格点,![]() 的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
的顶点在格点.请选择适当的格点用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
(1)如图![]() ,作
,作![]() 关于直线
关于直线![]() 的对称图形
的对称图形![]() ;
;
(2)如图![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如图![]() ,作
,作![]() 的中线
的中线![]() ;
;
(4)如图![]() ,在直线
,在直线![]() 上作出一条长度为
上作出一条长度为![]() 个单位长度的线段
个单位长度的线段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
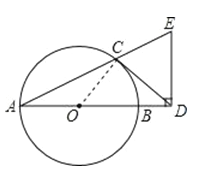
【题目】如图,AB 是⊙O 的直径,CD 与⊙O 相切于点 C,与 AB 的延长线交于点 D,DE⊥AD 且与AC 的延长线交于点 E.
(1)求证:DC=DE;
(2)若 AD=2ED,AB=3,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com