
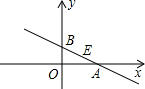
 如图,在平面直角坐标系xOy中,直线y=kx+b交x轴于点A,交y轴于点B,线段AB的中点E的坐标为(2,1).
如图,在平面直角坐标系xOy中,直线y=kx+b交x轴于点A,交y轴于点B,线段AB的中点E的坐标为(2,1). 解:(1)作EF⊥OA于点F.
解:(1)作EF⊥OA于点F.
|
|
| 1 |
| 2 |
|
|
| 4 |
| 3 |
| 4 |
| 3 |
|
|
| 4 |
| 3 |
| 4 |
| 3 |


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
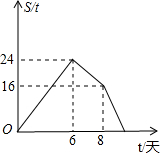 春耕期间,某农资门市部连续8天调进一批化肥进行销售,在开始调进化肥的第7天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:t)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是
春耕期间,某农资门市部连续8天调进一批化肥进行销售,在开始调进化肥的第7天开始销售.若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变,这个门市部的化肥存量S(单位:t)与时间t(单位:天)之间的函数关系如图所示,则该门市部这次化肥销售活动(从开始进货到销售完毕)所用时间是查看答案和解析>>
科目:初中数学 来源: 题型:
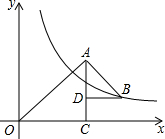 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=| k |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com