解:(1)因为∠A=60°,∠ABC=50°,
所以∠ACB=180°-∠A-∠ABC=70°.
∠ACD=∠A+∠ABC=110°.
因为EB平分∠ABC,EC平分∠ACD,
所以∠EBC=

∠ABC=25°,∠ACE=

∠ACD=55°.
所以∠E=180°-∠EBC-∠ACE-∠ACB
=180°-25°-55°-70°=30°.
(2)因为∠A=70°,∠ABC=60°,
所以∠ACB=180°-∠A-∠ABC=50°.
∠ACD=180°-∠ACB=180°-50°=130°.
因为EB平分∠ABC,EC平分∠ACD,
所以∠EBC=

∠ABC=30°,∠ACE=

∠ACD=75°.
所以∠E=180°-∠EBC-∠ACE-∠ACB
=180°-30°-50°-75°=35°.
同理可得∠E=35°.
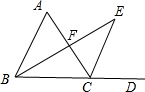
(3)猜测∠A=2∠E,下面说明理由:
因为EB平分∠ABC,EC平分∠ACD,
所以∠ABE=

∠ABC,∠ECD=

∠ACD.
因为∠A+∠ABE+∠AFB=∠E+∠ECF+∠EFC=180°,
又因为∠AFB=∠EFC,
所以∠A+∠ABE=∠E+∠ECF.
因为∠ECD=

∠ACD=

∠A+

∠ABC=

∠A+∠ABE.
所以∠A+∠ABE=∠E+

∠A+∠ABE.
所以∠E=

∠A.
分析:已知在△ABC中,∠ABC的角平分线和∠ACD的角平分线相交于点E,则得到∠EBC=

∠ABC,∠ECD=

∠ACD,再根据已知角的度数求出∠E的大小.
点评:本题考查角平分线的性质,以及三角形的外角等于不相邻的两个内角的和.

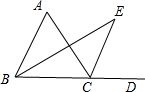 如图,在△ABC中,∠ABC的角平分线和∠ACD的角平分线相交于点E,
如图,在△ABC中,∠ABC的角平分线和∠ACD的角平分线相交于点E, ∠ABC=25°,∠ACE=
∠ABC=25°,∠ACE= ∠ACD=55°.
∠ACD=55°. ∠ABC=30°,∠ACE=
∠ABC=30°,∠ACE= ∠ACD=75°.
∠ACD=75°.
 ∠ABC,∠ECD=
∠ABC,∠ECD= ∠ACD.
∠ACD. ∠ACD=
∠ACD= ∠A+
∠A+ ∠ABC=
∠ABC= ∠A+∠ABE.
∠A+∠ABE. ∠A+∠ABE.
∠A+∠ABE. ∠A.
∠A. ∠ABC,∠ECD=
∠ABC,∠ECD= ∠ACD,再根据已知角的度数求出∠E的大小.
∠ACD,再根据已知角的度数求出∠E的大小.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为