练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在菱形ABCD中，对角线AC，BD相交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE相交于点E，若AB=10，AC=12，求四边形CODE的周长．

    【答案】28

    【解析】

    首先证明四边形CODE是平行四边形，然后证明∠DOC=90°可得到四边CODE是矩形，然后证明CO=AO=6，∠AOB=90°，运用勾股定理求出BO，即可解决问题．

    解：∵CE∥BD，DE∥AC，∴四边形CODE是平行四边形．

    ∵四边形ABCD是菱形

    ∴∠DOC=90°，∴四边形CODE是矩形；

    ∵四边形ABCD为菱形，∴AO=OC= AC=6，OD=OB，∠AOB=90°，由勾股定理得：

    BO2=AB2﹣AO2，而AB=10，∴DO=BO==8，由（1）得四边形CODE是矩形，∴四边形CODE的周长=2（6+8）=28．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，∠B=90°，AB∥CD，M为BC边上的一点，且AM平分∠BAD，DM平分∠ADC．

    求证：（1）AM⊥DM；

    （2）M为BC的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线l：y=mx﹣m+1（m为常数，且m≠0）与坐标轴交于A、B两点，若△AOB（O是原点）的面积恰为2，则符合要求的直线l有（ ）
    A.1条
    B.2条
    C.3条
    D.4条

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角梯形ABCD中， ， ， ， ．

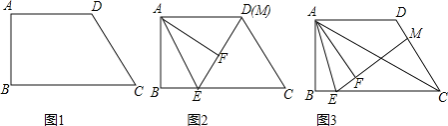
    （1）如图1，连接AC，求证：CA是的平分线；

    （2）线段BC上一点E，将 沿AE翻折，点B落到点F处，射线EF与线段CD交于点M．

    ①如图2，当点M与点D重合时，求证： ；

    ②如图3，当点M不与点D重合时，求证： ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校八（1）班同学为了解2018年某小区家庭月均用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理，请解答以下问题：

    （1）本次调查采用的调查方式是________（填“普查”或“抽样调查”），样本容量是________；

    （2）补全频数分布直方图：

    （3）若将月均用水量的频数绘成扇形统计图，则月均用水量“”的圆心角度数是________；

    （4）若该小区有5000户家庭，求该小区月均用水量超过的家庭大约有多少户？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算或化简：

    （1）2﹣1+

    （2）2x2y（﹣3xy）÷（xy）2

    （3）（﹣2a）（3a2﹣a+3）

    （4）（x+3）（x+4）﹣（x﹣1）2

    （5）[2a3x2（a﹣2x）﹣a2x2]÷（﹣ax）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，C(0，5)，D(a，5)（a ＞0），A、B 在 x 轴上，∠1=∠D，求证：∠ACB+∠BED=180°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】推理填空：如图，E点为DF上的点，B为AC上的点， ，那么，请完成它成立的理由

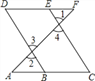
    解： ______

    又

    ______

    ______ ______ ______

    ______

    ______

    ______

    ______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在△ABC中，BD是△ABC的角平分线，点D在AC上，DE∥BC，交AB于点E，∠A＝50°，∠ADB＝110°，求△BDE各内角的度数；

    （2）完成下列推理过程．

    已知：如图2，AD⊥BC，EF⊥BC，∠1＝∠2，求证：DG∥AB．推理过程：因为AD⊥BC，EF⊥BC（已知），

    所以∠EFB＝∠ADB＝90°（________）．

    所以EF∥AD（同位角相等，两直线平行）．

    所以∠1＝∠BAD（________）．

    因为∠1＝∠2（已知），

    所以________=________（等量代换）．

    所以DG∥AB（内错角相等，两直线平行）．

    查看答案和解析>>

    同步练习册答案