
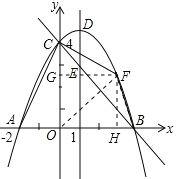
【题目】(12分)如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.

(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
【答案】(1)y=-![]()
![]() +x+4;(2)不存在.
+x+4;(2)不存在.
【解析】
试题首先设抛物线的解析式为一般式,将点C和点A意见对称轴代入求出函数解析式;本题利用假设法来进行证明,假设存在这样的点,然后设出点F的坐标求出FH和FG的长度,然后得出面积与t的函数关系式,根据方程无解得出结论.
试题解析:(1)∵抛物线y=a![]() +bx+c(a≠0)过点C(0,4) ∴C=4①
+bx+c(a≠0)过点C(0,4) ∴C=4①
∵-![]() =1 ∴b=-2a② ∵抛物线过点A(-2,0) ∴4a-2b+c=0 ③
=1 ∴b=-2a② ∵抛物线过点A(-2,0) ∴4a-2b+c=0 ③
由①②③解得:a=-![]() ,b=1,c=4 ∴抛物线的解析式为:y=-
,b=1,c=4 ∴抛物线的解析式为:y=-![]()
![]() +x+4
+x+4
(2)不存在 假设存在满足条件的点F,如图所示,连结BF、CF、OF,过点F作FH⊥x轴于点H,FG⊥y轴于点G.设点F的坐标为(t,![]() +t+4),其中0<t<4 则FH=
+t+4),其中0<t<4 则FH=![]() +t+4 FG=t
+t+4 FG=t
∴△OBF的面积=![]() OB·FH=
OB·FH=![]() ×4×(
×4×(![]() +t+4)=-
+t+4)=-![]() +2t+8 △OFC的面积=
+2t+8 △OFC的面积=![]() OC·FG=2t
OC·FG=2t
∴四边形ABFC的面积=△AOC的面积+△OBF的面积+△OFC的面积=-![]() +4t+12
+4t+12
令-![]() +4t+12=17 即-
+4t+12=17 即-![]() +4t-5=0 △=16-20=-4<0 ∴方程无解
+4t-5=0 △=16-20=-4<0 ∴方程无解
∴不存在满足条件的点F


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=![]() x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
x2+bx+c与x轴交于A(-1,0)、B两点(A在B左),y轴交于点C(0,-3).
(1)求抛物线的解析式;
(2)若点D是线段BC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在x轴上,点P在抛物线上.是否存在以B、C、E、P为顶点且以BC为一边的平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举行开业酬宾活动,设立了两个可以自由转动的转盘(如图所示,两个转盘均被等分),并规定:顾客购买满188元的商品,即可任选一个转盘转动一次,转盘停止后,指针所指区域内容即为优惠方式;若指针所指区域空白,则无优惠.已知小张在该商场消费300元
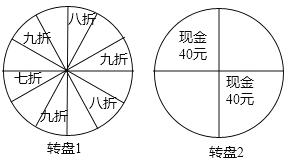
(1)若他选择转动转盘1,则他能得到优惠的概率为多少?
(2)选择转动转盘1和转盘2,哪种方式对于小张更合算,请通过计算加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题成立的有( )
①勾股数是三个正整数 ②全等三角形的三条对应边分别相等
③如果两个实数相等,那么它们的平方相等 ④平行四边形的两组对角分别相等
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
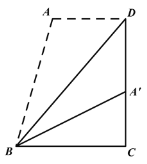
【题目】如图,四边形 ABCD 中,AD∥BC,DC⊥BC,将四边形沿对角线 BD 折叠,点 A 恰好落在 DC 边上的 点 A'处,若∠A'BC=20°,则∠A'BD 的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】腰长为4的等腰直角![]() 放在如图所示的平面直角坐标系中,点A、C均在y轴上,C(0,2),∠ACB=90
放在如图所示的平面直角坐标系中,点A、C均在y轴上,C(0,2),∠ACB=90![]() ,AC=BC=4,平行于y轴的直线x=-2交线段AB于点D,点P是直线x=-2上一动点,且在点D的上方,当
,AC=BC=4,平行于y轴的直线x=-2交线段AB于点D,点P是直线x=-2上一动点,且在点D的上方,当![]() 时,以PB为直角边作等腰直角
时,以PB为直角边作等腰直角![]() ,则所有符合条件的点M的坐标为________.
,则所有符合条件的点M的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
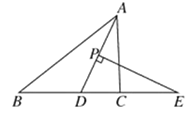
【题目】如图,在![]() 中,
中,![]() 平分
平分![]() .
.
(1)若![]() 为线段
为线段![]() 上的一个点,过点
上的一个点,过点![]() 作
作![]() 交线段
交线段![]() 的延长线于点
的延长线于点![]() .
.
①若![]() ,
,![]() ,则
,则![]() _______
_______![]() ;
;
②猜想![]() 与
与![]() 、
、![]() 之间的数量关系,并给出证明.
之间的数量关系,并给出证明.
(2)若![]() 在线段
在线段![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,请你直接写出
,请你直接写出![]() 与
与![]() 、
、![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
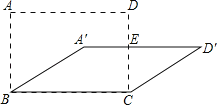
【题目】如图,若将四根木条钉成的矩形木框ABCD变形为平行四边形A′BCD′,并使其面积为矩形ABCD面积的一半,若A′D′与CD交于点E,且AB=2,则△ECD′的面积是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com