解:∵AC与圆O相切,且D为切点,
∴OD⊥AC,
在直角三角形AOD中,AD=2,AE=1,
设OD=x,OA=AE+EO=1+x,
根据勾股定理得:OA
2=AD
2+OD
2,即(1+x)
2=2
2+x
2,
解得:x=1.5,
∴OD=1.5,EB=3,AO=2.5,AB=AE+EB=1+3=4,
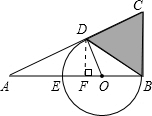
过点D作DF⊥AB,如图所示:
∴S
△ADO=

AD•DO=

AO•DF,
∴DF=
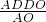
=1.2,
∴S
△ADB=

AB•DF=2.4,
∵∠ABC=90°,
∴BC与圆O相切,又CD与圆O相切,
∴CB=CD,
在直角三角形ABC中,设CB=CD=y,
∴AC=AD+DC=2+y,AB=4,
根据勾股定理得:AC
2=AB
2+BC
2,即(2+y)
2=4
2+y
2,
解得:y=3,
∴CB=CD=3,
∴S
△ABC=

AB•BC=6,
则S
△BCD=S
△ABC-S
△ADB=6-2.4=3.6.
分析:由AC与圆O相切,根据切线的性质得到OD与AC垂直,可得出三角形AOD为直角三角形,设OD=OE=x,用AO=AE+EO,由AE的长及设出的OE表示出OA,再由AD的长,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出OD,EB,AO及AB的长,过点D作DF垂直于AB,由直角三角形AOD的面积由斜边OA与DF乘积的一半来求,也可以由AD与DO乘积的一半来求,进而求出DF的长,即为三角形ADB中AB边上的高,求出三角形ADB的面积,再由∠ABC=90°,判定出BC为圆的切线,又CD也为圆的切线,根据切线长定理得到CD=CB,可设CD=CB=y,表示出AC,再由AB的长,在直角三角形ABC中,利用勾股定理列出关于y的方程,求出方程的解得到y的值,确定出CB的长,利用两直角边AB及BC乘积的一半求出三角形ABC的面积,用三角形ABC的面积减去三角形ABD的面积,即可求出三角形BCD的面积.
点评:此题考查了切线的性质与判定,勾股定理,三角形面积的求法,以及切线长定理,熟练掌握性质及定理是解本题的关键.

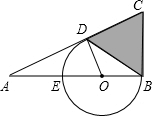 如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,求S△BCD.
如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,AD=2,AE=1,求S△BCD.
 AD•DO=
AD•DO= AO•DF,
AO•DF,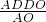 =1.2,
=1.2, AB•DF=2.4,
AB•DF=2.4, AB•BC=6,
AB•BC=6,

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为