
(1)见解析 (2)3
【解析】
试题分析:根据AE⊥CD和AH⊥BF可得∠B=∠H,根据同弧所对的圆周角相等可得∠B=∠C,从而得出∠C=∠H,得出结论;(2)连接OA,设DE=x,OE=y,根据垂径定理可得:AE= ,根据等腰三角形的性质可得CE=BE,然后根据直角△AOE的垂径定理进行求解.
,根据等腰三角形的性质可得CE=BE,然后根据直角△AOE的垂径定理进行求解.
试题解析:(1)∵AE⊥CD,AH⊥BF ∴∠B=∠H ∵∠C=∠B ∴∠C=∠H ∴AC=AH
、连接AO,∵AC=AH,CD⊥AB ∴AE=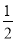 AB=
AB= ,CE=EH
,CE=EH
设ED=x,OE=y ∴OA=OC=OD=x+y ∴EH=CE=x+2y ∴OH=x+3y=5
∵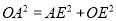 即
即 ∴x=2,y=1
∴x=2,y=1
∴⊙O的半径为:x+y=2+1=3.
考点:垂径定理、等腰三角形的性质、勾股定理.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:初中数学 来源:2013-2014学年江苏省九年级上学期期末考试数学试卷(解析版) 题型:解答题
如图所示,⊙O 的半径是4,PA、PB分别与⊙O相切于点A、点B,若PA与PB之间的夹角∠APB=60°,
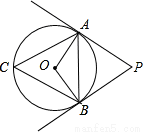
(1)若点C是圆上的一点,试求∠ACB的大小;
(2)求△ABP的周长
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级上学期期末考试数学试卷(解析版) 题型:选择题
已知二次函数 的图象如图所示,现有下列结论:①
的图象如图所示,现有下列结论:① ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ,则其中结论正确的个数是( )
,则其中结论正确的个数是( )

A、2 B、3 C、4 D、5
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:解答题
(本小题满分10分)如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=1:2,D(3,0)直线CD垂直于直线AB于点P,交x轴于点D。

(1)求出点A、点B的坐标。
(2)请求出直线CD的解析式。
(3)若点M为坐标平面内任意一点,在直线AB上是否存在这样的点M,使以点B、D、M为顶点的三角形与△AOB相似,若存在,请直接写出点M的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与 轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为
轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为 ,则点P的坐标为 ____________.
,则点P的坐标为 ____________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年黑龙江省牡丹江管理局北斗星协会九年级中考三模数学试卷(解析版) 题型:填空题
2014年5月20日是全国学生营养日,将数20140520精确到万位后,请用科学记数表示为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com