
为深化“携手节能低碳,共建碧水蓝天”活动,发展“低碳经济”,某单位进行技术革新,让可再生资源重新利用.今年1月份,再生资源处理量为40吨,从今年1月1日起,该单位每月再生资源处理量每一个月将提高10吨.月处理成本(元)与月份之间的关系可近似地表示为: ,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).
,每处理一吨再生资源得到的新产品的售价定为100元.若该单位每月再生资源处理量为y(吨),每月的利润为w(元).
(1)分别求出y与x,w与x的函数关系式;
(2)在今年内该单位哪个月获得利润达到5800元?
(3)随着人们环保意识的增加,该单位需求的可再生资源数量受限.今年三月的再生资源处理量比二月份减少了m%,该新产品的产量也随之减少,其售价比二月份的售价增加了 %.四月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了
%.四月份,该单位得到国家科委的技术支持,使月处理成本比二月份的降低了 %.如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上,其利润比二月份的利润减少了60元,求m的值.
%.如果该单位四月份在保持三月份的再生资源处理量和新产品售价的基础上,其利润比二月份的利润减少了60元,求m的值.
(1) y=10x+30,w=-50x2+900x+2550;(2)5;(3)10.
解析试题分析:(1)首先根据表格求出y与x的函数关系式,然后利用已知条件即可得到P与x的函数关系式;
(2)根据(1)所求可以进而得到利润与x之间的函数关系式,即可求解;
(3)首先根据已知条件可以分别求出:二月处理量、二月成本、二月利润,接着利用已知条件即可列出方程100×50(1-m%)(1+0.6m%)-850×(1-20%)=50×100-850-60,解方程即可解决问题.
试题解析::解:(1)将(1,40),(2,50)代入y=kx+b,
得: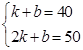 ,解得:
,解得: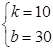
故每月再生资源处理量y(吨)与x月份之间的关系式为:y=10x+30,
w=100y-p
=100(10x+30)-(50x2+100x+450)
=-50x2+900x+2550
(2)由-50x2+900x+2550=5800得:
x2-18x+65=0
∴x1=13,x2=5
∵x≤12,
∴x=5
∴在今年内该单位第5个月获得利润达到5800元.
(3)二月份再生资源处理量:40+10=50吨,
二月成本:P=50×22+100×2+450=850元,
100×50(1-m%)(1+0.6m%)-950×(1-20%)=4050,
令m%=t,则300t2+200t-23=0
∴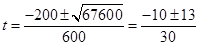
∵t>0
∴t=0.1
∴m%=0.1,即m=10.
考点:二次函数的应用.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:填空题
(2013年四川绵阳4分)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:
①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n< ;④3|a|+|c|<2|b|.
;④3|a|+|c|<2|b|.
其中正确的结论是 (写出你认为正确的所有结论序号).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“丹棱冻粑”是眉山著名特色小吃,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一次函数y=x–3的图象与 轴,
轴, 轴分别交于点
轴分别交于点 .一个二次函数y=x2+bx+c的图象经过点
.一个二次函数y=x2+bx+c的图象经过点 .
.
(1)求点 的坐标,并画出一次函数y=x–3的图象;
的坐标,并画出一次函数y=x–3的图象;
(2)求二次函数的解析式并求其图像顶点C的坐标.
(3)求 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在Rt△ABC中,∠BAC=90°,∠B=60°,BC=16cm,AD是斜边BC上的高,垂足为D,BE=1cm.点M从点B出发沿BC方向以1cm/s的速度运动,点N从点E出发,与点M同时同方向以相同的速度运动,以MN为边在BC的上方作正方形MNGH.点M到达点D时停止运动,点N到达点C时停止运动.设运动时间为t(s).
(1)当t为何值时,点G刚好落在线段AD上?
(2)设正方形MNGH与Rt△ABC重叠部分的图形的面积为S,当重叠部分的图形是正方形时,求出S关于t的函数关系式并写出自变量t的取值范围.
(3)设正方形MNGH的边NG所在直线与线段AC交于点P,连接DP,当t为何值时,△CPD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定:公共租赁住房和廉租住房并轨运行(以下简称并轨房),计划10年内解决低收入人群住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百万平方米,且y与x的函数关系式为y=-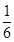 x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
| 时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
| 单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系中, 抛物线
 +
+ 与直线
与直线 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
(1)如图1,当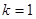 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线
 +
+ 
 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:矩形ABCD中,M为BC边上一点, AB=BM=10,MC=14,如图1,正方形EFGH的顶点E和点B重合,点F、G、H分别在边AB、AM、BC上.如图2,P为对角线AC上一动点,正方形EFGH从图1的位置出发,以每秒1个单位的速度沿BC向点C匀速移动;同时,点P从C点出发,以每秒1个单位的速度沿CA向点A匀速移动.当点F到达线段AC上时,正方形EFGH和点P同时停止运动.设运动时间为t秒,解答下列问题:
(1)在整个运动过程中,当点F落在线段AM上和点G落在线段AC上时,分别求出对应t的值;
(2)在整个运动过程中,设正方形 与
与 重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
重叠部分面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围;
(3)在整个运动过程中,是否存在点P,使 是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
是以DG为腰的等腰三角形?若存在,求出t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图①,已知二次函数的解析式是y=ax2+bx(a>0),顶点为A(1,-1).
(1)a= ;
(2)若点P在对称轴右侧的二次函数图像上运动,连结OP,交对称轴于点B,点B关于顶点A的对称点为C,连接PC、OC,求证:∠PCB=∠OCB;
(3)如图②,将抛物线沿直线y=-x作n次平移(n为正整数,n≤12),顶点分别为A1,A2,…,An,横坐标依次为1,2,…,n,各抛物线的对称轴与x轴的交点分别为D1,D2,…,Dn,以线段AnDn为边向右作正方形AnDnEnFn,是否存在点Fn恰好落在其中的一个抛物线上,若存在,求出所有满足条件的正方形边长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com