
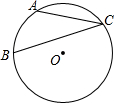
 如图,点A、B、C在半径为1的⊙O上,$\widehat{AB}$的长为$\frac{2}{5}$π,则∠ACB的大小是36°.
如图,点A、B、C在半径为1的⊙O上,$\widehat{AB}$的长为$\frac{2}{5}$π,则∠ACB的大小是36°. 分析 连结OA、OB.先由$\widehat{AB}$的长为$\frac{2}{5}$π,利用弧长计算公式求出∠AOB=72°,再根据在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半得到∠ACB=$\frac{1}{2}$∠AOB=36°.
解答 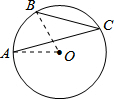 解:连结OA、OB.设∠AOB=n°.
解:连结OA、OB.设∠AOB=n°.
∵$\widehat{AB}$的长为$\frac{2}{5}$π,
∴$\frac{n×π×1}{180}$=$\frac{2}{5}$π,
∴n=72,
∴∠AOB=72°,
∴∠ACB=$\frac{1}{2}$∠AOB=36°.
故答案为:36°.
点评 本题考查了弧长公式:l=$\frac{nπr}{180}$(弧长为l,圆心角度数为n,圆的半径为r),同时考查了圆周角定理.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:选择题
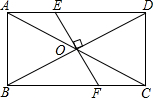 如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2$\sqrt{3}$,∠AEO=120°,则FC的长度为( )
如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2$\sqrt{3}$,∠AEO=120°,则FC的长度为( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中有等腰Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(n,2).
如图,在平面直角坐标系中有等腰Rt△ABC,∠A=90°,AB=AC,A(-2,0),B(0,1),C(n,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
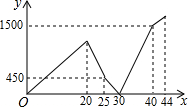 小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距1740米.
小兵早上从家匀速步行去学校,走到途中发现数学书忘在家里了,随即打电话给爸爸,爸爸立即送书去,小兵掉头以原速往回走,几分钟后,路过一家书店,此时还未遇到爸爸,小兵便在书店挑选了几支笔,刚付完款,爸爸正好赶到,将书交给了小兵.然后,小兵以原速继续上学,爸爸也以原速返回家.爸爸到家后,过一会小兵才到达学校.两人之间的距离y(米)与小兵从家出发的时间x(分钟)的函数关系如图所示.则家与学校相距1740米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解浙江省中学教师的健康情况 | B. | 了解台州市初中生的兴趣爱好 | ||
| C. | 了解路桥区中小学生的睡眠时间 | D. | 为定制校服了解我校学生身高情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
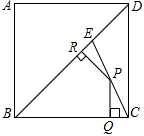 如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( )
如图,E为边长为2的正方形ABCD的对角线上一点,BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于R,则PQ+PR的值为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2017 | B. | 2020 | C. | 2019 | D. | 2018 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b≥-1 | B. | b≤-1 | C. | b≥-2 | D. | b≤-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com