
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,P为BA延长线上一点,连接CA、CD、AD,且∠PCA=∠ADC,CE⊥AB于E,并延长交AD于F.

(1)求证:PC为⊙O的切线;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,求PA的长.
,求PA的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)如图(见解析),先根据圆周角定理可得![]() ,再根据等腰三角形的性质、三角形的内角和定理可得
,再根据等腰三角形的性质、三角形的内角和定理可得![]() ,然后根据角的和差可得
,然后根据角的和差可得![]() ,最后根据圆的切线的判定即可得证;
,最后根据圆的切线的判定即可得证;
(2)如图(见解析),先根据圆周角定理可得![]() ,从而可得
,从而可得![]() ,再根据相似三角形的判定与性质即可得证;
,再根据相似三角形的判定与性质即可得证;
(3)先根据圆周角定理、直角三角形的性质可得![]() ,再根据相似三角形的判定与性质可得
,再根据相似三角形的判定与性质可得![]() ,从而可得
,从而可得![]() ,又根据圆周角定理、正切三角函数可得
,又根据圆周角定理、正切三角函数可得![]() ,然后设
,然后设![]() ,由题(2)的结论可得
,由题(2)的结论可得![]() ,最后根据相似三角形的性质可得
,最后根据相似三角形的性质可得![]() ,由此即可得出答案.
,由此即可得出答案.
(1)如图,连接OC
由圆周角定理得:![]() ,即
,即![]()
![]()
![]()
![]()
![]() ,即
,即![]()
又![]() 是⊙O的半径
是⊙O的半径
![]() PC是⊙O的切线;
PC是⊙O的切线;
(2)如图,连接BC
由圆周角定理得:![]()
![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]()
即![]() ;
;
(3)![]() ,即
,即![]()
![]()
由圆周角定理得:![]()
![]()
![]()
又![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,即
,即![]()
![]()
![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]()
![]() ,即
,即![]()
解得![]()
![]() ,
,![]()
设![]() ,则
,则![]()
由(2)可知,![]() ,即
,即![]()
又由(2)可知,![]()
![]() ,即
,即![]()
解得![]() 或
或![]()
经检验,![]() 是所列方程的根,
是所列方程的根,![]() 是所列方程的增根
是所列方程的增根
故PA的长为![]() .
.



 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
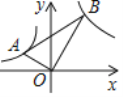
【题目】在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点O重合,顶点A,B恰好分别落在函数![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上,若sin∠BAO =
(x>0)的图象上,若sin∠BAO = ![]() ,则k的值为__________.
,则k的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传普及新冠肺炎防治知识,引导学生做好防控.某校举行了主题为“防控新冠,从我做起”的线上知识竞赛活动,测试内容为20道判断题,每道题5分,满分100分,为了解八、九年级学生此次竞赛成绩的情况,分别随机在八、九年级各抽取了20名参赛学生的成绩.已知抽查得到的八年级的数据如下:80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
为了便于分析数据,统计员对八年级数据进行了整理,得到了表一:
成绩等级 | 分数(单位:分) | 学生数 |
D等 | 60<x≤70 | 5 |
C等 | 70<x≤80 | a |
B等 | 80<x≤90 | b |
A等 | 90<x≤100 | 2 |
九年级成绩的平均数、中位数、优秀率如下:(分数80分以上、不含80分为优秀)
年级 | 平均数 | 中位数 | 优秀率 |
八年级 | 77.5 | c | m% |
九年级 | 76 | 82.5 | 50% |
(1)根据题目信息填空:a= ,c= ,m= ;
(2)八年级小宇和九年级小乐的分数都为80分,请判断小宇、小乐在各自年级的排名哪位更靠前?请简述你的理由;
(3)若九年级共有600人参加参赛,请估计九年级80分以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )

A. 3![]() km B. 3
km B. 3![]() km C. 4km D. (3
km C. 4km D. (3![]() -3)km
-3)km
查看答案和解析>>
科目:初中数学 来源: 题型:
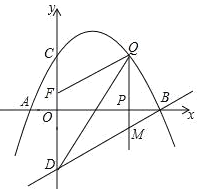
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于![]() 轴对称,点P是
轴对称,点P是![]() 轴上的一个动点,设点P的坐标为(
轴上的一个动点,设点P的坐标为(![]() ,0),过点P做
,0),过点P做![]() 轴的垂线l交抛物线于点Q,交直线BD于点M.
轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB运动过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,![]() ),当点P在
),当点P在![]() 轴上运动时,试求
轴上运动时,试求![]() 为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,对角线AC、BD相交于点O,E是边AB上的一个动点(不与A、B重合),连接EO并延长,交CD于点F,连接AF,CE,下列四个结论中:
①对于动点E,四边形AECF始终是平行四边形;
②若∠ABC<90°,则至少存在一个点E,使得四边形AECF是矩形;
③若AB>AD,则至少存在一个点E,使得四边形AECF是菱形;
④若∠BAC=45°,则至少存在一个点E,使得四边形AECF是正方形.
以上所有正确说法的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图11,一转盘被等分成三个扇形,上面分别标有关-1,1,
2中的一个数,指针位置固定,转动转盘后任其自由停止,这时,鞭个扇形恰好停在指针所
指的位置,并相应得到这个扇形上的数(若指针恰好指在等分线上,当做指向右边的扇形).
⑴若小静转动转盘一次,求得到负数的概率;
⑵小宇和小静分别转动一次,若两人得到的数相同,则称两人“不谋而合”,用列表法(或画树形图)求两人“不谋而合”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.①②④C.②③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
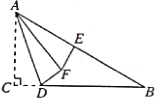
【题目】如图,已知在△ABC中,![]() ,
,![]() ,
,![]() ,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
,点E为AB的中点,D为BC边上的一动点,把△ACD沿AD折叠,点C落在点F处,当△AEF为直角三角形时,CD的长为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com