
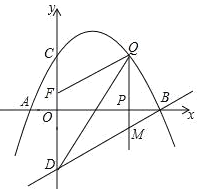
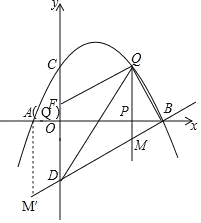
����Ŀ����ͼ����֪�����߾�����A����1��0����B��4��0����C��0��2�����㣬��D���C����![]() ��Գƣ���P��
��Գƣ���P��![]() ���ϵ�һ�����㣬���P������Ϊ��
���ϵ�һ�����㣬���P������Ϊ��![]() ��0��������P��
��0��������P��![]() ��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ����BOD�ס�QBM�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����֪��F��0��![]() ��������P��
��������P��![]() �����˶�ʱ������
�����˶�ʱ������![]() Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() ����3��-1��3��
����3��-1��3��![]() ��
��![]()
��������
��1�����ô���ϵ������⼴�ɣ�
��2����������ͼ��֪��DOB�ס�MBQ����MBQ�ס�QPB����BOD�ס�QPB������![]() ���ɵ������ɵ�
���ɵ������ɵ�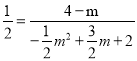 ����֮���ɵô�ʱmֵ��
����֮���ɵô�ʱmֵ��
��3�������ô���ϵ�������ֱ��BD�Ľ���ʽ�������õ���Q��M�����꣬����QM��DF���ı���DMQF��ƽ���ı���֪QM=DF���ݴ��г�����m�ķ��̣���֮����.
��1���������߹���A����1��0����B��4��0���������ʽΪy=a��x+1����x��4��������C��0��2�����룬�ã���4a=2����ã�a=��![]() ��
��
�������߽���ʽΪy=��![]() ��x+1����x��4��=��
��x+1����x��4��=��![]() ��
��
��2������ ��������
�ߡ�MBQ=90���MBP+��PBQ=90
�ߡ�MPB=��BPQ=90��
���MBQ+��BMP=90��
���PBQ=��BMP��
����MBQ�ס�QPB��
�ߡ�DOB�ס�MBQ��
���BOD�ס�QPB��
��![]() ����
����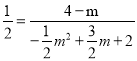 ��
��
��ã�m1=3��m2=4��
��m=4ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
��m=3����Q��������3��2����
��3��������֪��D����Ϊ��0����2������ֱ��BD����ʽΪy=kx+b��
��B��4��0����D��0����2�����룬�ã�![]() ����ã�
����ã�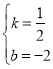 ��
��
��ֱ��BD����ʽΪy=![]() x��2����QM��x�ᣬP��m��0����
x��2����QM��x�ᣬP��m��0����
��Q��m��![]() ����M��m��
����M��m��![]() m��2����
m��2����
��QM=|![]() ����
����![]() m��2��|=|��
m��2��|=|��![]() m2+m+4|��
m2+m+4|��
��F��0��![]() ����D��0����2������DF=
����D��0����2������DF=![]() ����QM��DF��
����QM��DF��
�൱|��![]() m2+m+4|=
m2+m+4|=![]() ʱ���ı���DMQF��ƽ���ı��Σ���ã�m=��1��m=3��
ʱ���ı���DMQF��ƽ���ı��Σ���ã�m=��1��m=3��![]()
��m=��1��m=3��![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����÷��ѧΪ�˷ḻѧ���Ŀ�������ƻ�����Χ����й����幩������ȤС��ʹ�ã�������3��Χ���5���й���������98Ԫ��������8��Χ���3���й���������158Ԫ����1����ÿ��Χ���ÿ���й����������Ԫ����2����÷��ѧ��������Χ����й����干40�����ܷ��ò�����550Ԫ����ô��÷��ѧ�����Թ�����ٸ�Χ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=x+3�ֱ�x�ᡢy����A��C���㣬������y=ax2+bx+c��a��0��������A��C���㣬��x�ύ�ڵ�B��1��0����
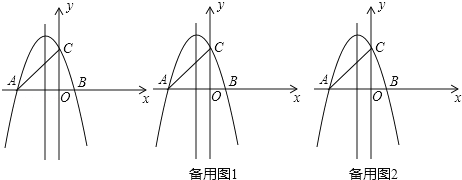
��1���������ߵĽ���ʽ��
��2����DΪֱ��AC��һ�㣬��EΪ��������һ�㣬��D��E����ĺ����궼Ϊ2����FΪx���ϵĵ㣬���ı���ADEF��ƽ���ı��Σ���ֱ��д����F�����ꣻ
��3������P���߶�AC�ϵ�һ�����㣬����P��x��Ĵ��ߣ����������ڵ�Q������AQ��CQ������ACQ����������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�ǵȱ������Σ���D��E�ֱ���AC��BC�ϣ���CD=BE��

��1����֤����ABE�ա�BCD��
��2�������AFB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BC=4����NΪ��DC��һ���㣨����C��D�غϣ�������BN����C����ֱ��BN�ĶԳƵ�C������B C���� C��N����C��ǡ������ABD�ı���ʱ��CN�ij�Ϊ__________��
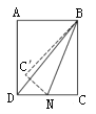
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C��D�ڡ�O�ϣ�PΪBA�ӳ�����һ�㣬����CA��CD��AD���ҡ�PCA����ADC��CE��AB��E�����ӳ���AD��F��

��1����֤��PCΪ��O�����ߣ�
��2����֤��![]() ��
��
��3����![]() ��
��![]() ����PA�ij���
����PA�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪Rt��ABC�У���ACB=90�㣬CD��б��AB�ϵ����ߣ�����A��AE��CD��AE�ֱ���CD��CB�ཻ�ڵ�H��E��AH=2CH.
(1)��sinB��ֵ��
(2)���CD=![]() ����BE��ֵ.
����BE��ֵ.
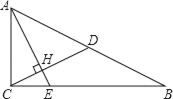
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ѧ��ijУΪ���˽���꼶���Ͻ�ѧ�ڼ�ѧ��֪ʶ������������������Ͻ�ѧ�������в��ԣ�����ʦ���ݲ��Խ�����Ա��ಿ��ѧ�������˷��������������Ϊ���࣬![]() �����㣻
�����㣻![]() �����ã�
�����ã�![]() ���ϸ�
���ϸ�![]() �����ϸ���������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺
�����ϸ���������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺
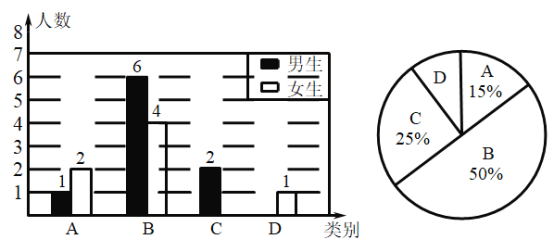
��1������ʦһ��������_________��ͬѧ��
��2��![]() ����ռ����Բ�ĽǵĶ�����_________��
����ռ����Բ�ĽǵĶ�����_________��
��3������������ͳ��ͼ����������
��4��Ϊ�˹�ͬ����������ʦ��ӱ������![]() ���
���![]() ��ѧ���и����ѡȡһλͬѧ������һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ�ö���Ůͬѧ�ĸ��ʣ�
��ѧ���и����ѡȡһλͬѧ������һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ�ö���Ůͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڷ����¹�״�����ڼ䣬�����ҽ�ÿ��ֵ�����Խ��Խ��ijҩ���һ����![]() Ԫ����ҽ�ÿ������ɸ����ڶ�������
Ԫ����ҽ�ÿ������ɸ����ڶ�������![]() Ԫ�����ÿ���֣����ڶ���ÿ�����ֵĽ����ǵ�һ�ν��۵�
Ԫ�����ÿ���֣����ڶ���ÿ�����ֵĽ����ǵ�һ�ν��۵�![]() ���������������ȵ�һ����
���������������ȵ�һ����![]() ����
����
��1�����һ�κ͵ڶ��ηֱ���ҽ�ÿ�������Ϊ���ٸ���
��2��ҩ���һ�ι������ֺ�����ÿ��![]() Ԫ�ļ۸���ۣ�������
Ԫ�ļ۸���ۣ�������![]() �����ڶ���ͬ����֣����ڽ�������ˣ�ҩ�꽫���ֵ��ۼ�Ҳ������ÿ��
�����ڶ���ͬ����֣����ڽ�������ˣ�ҩ�꽫���ֵ��ۼ�Ҳ������ÿ��![]() Ԫ��������������
Ԫ��������������![]() ������ҽԺҽ�����ʽ�ȱ�������ѻ�ÿ�����������
������ҽԺҽ�����ʽ�ȱ�������ѻ�ÿ�����������![]() Ԫ��ʣ��ȫ���Ŀ��־�������ҽԺ����ҩ��������������ж��ٸ���
Ԫ��ʣ��ȫ���Ŀ��־�������ҽԺ����ҩ��������������ж��ٸ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com