
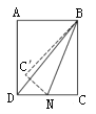
【题目】如图,在矩形ABCD中,AB=3,BC=4,点N为边DC上一动点(不与C、D重合),连接BN,作C关于直线BN的对称点C′连接B C′, C′N,当C′恰好在△ABD的边上时,CN的长为__________.
科目:初中数学 来源: 题型:
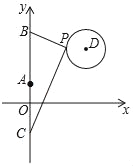
【题目】如图,在平面直角坐标系中,已知点A(0,1)、点B(0,1+t)、C(0,1﹣t)(t>0),点P在以D(3,5)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则t的最小值是( )
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现任意三个连续的整数中,最大数与最小数这两个数的平方差是4的倍数;
验证:(1) ![]() 的结果是4的几倍?
的结果是4的几倍?
(2)设三个连续的整数中间的一个为n,计算最大数与最小数这两个数的平方差,并说明它是4的倍数;
延伸:说明任意三个连续的奇数中,最大的数与最小的数这两个数的平方差是8的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
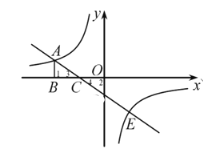
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 图象上一点,
图象上一点,![]() 轴于点
轴于点![]() ,
,![]() 是
是![]() 的中点.一次函数
的中点.一次函数![]() 经过
经过![]() ,
,![]() 两点,
两点,![]() .
.
(1)求反比例函数和一次函数的解析式.
(2)画出反比例函数的另一支图象,写出自变量![]() 取何值时,使反比例函数的函数值大于一次函数的函数值.
取何值时,使反比例函数的函数值大于一次函数的函数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
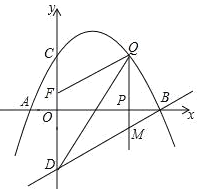
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于![]() 轴对称,点P是
轴对称,点P是![]() 轴上的一个动点,设点P的坐标为(
轴上的一个动点,设点P的坐标为(![]() ,0),过点P做
,0),过点P做![]() 轴的垂线l交抛物线于点Q,交直线BD于点M.
轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB运动过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,![]() ),当点P在
),当点P在![]() 轴上运动时,试求
轴上运动时,试求![]() 为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax﹣3a(a≠0)与x轴交于A、B两点,与y轴交于点C,且OA=OC,直线y=﹣x与该抛物线交于E,F两点.
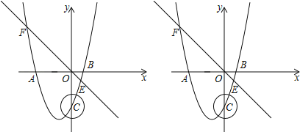
(1)求抛物线的解析式.
(2)P是直线EF下方抛物线上的一个动点,作PH⊥EF于点H,求PH的最大值.
(3)以点C为圆心,1为半径作圆,⊙C上是否存在点D,使得△BCD是以CD为直角边的直角三角形?若存在,直接写出D点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与x轴相交于点A和点B(点A在点B的左侧),与y轴相交于点C.一次函数
的图像与x轴相交于点A和点B(点A在点B的左侧),与y轴相交于点C.一次函数![]() 的图像与y轴相交于点D,其中
的图像与y轴相交于点D,其中![]() .
.
(1)分别求出A、B、C三点的坐标(可以用含有字母a的代数式表示).
(2)点P与点C关于抛物线的对称轴成轴对称,点Q为抛物线上的一个动点.
①试说明点P在直线![]() 的图像上.
的图像上.
②若点Q在抛物线上有且只有三个位置满足![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com