
【题目】已知二次函数![]() 的图像与x轴相交于点A和点B(点A在点B的左侧),与y轴相交于点C.一次函数
的图像与x轴相交于点A和点B(点A在点B的左侧),与y轴相交于点C.一次函数![]() 的图像与y轴相交于点D,其中
的图像与y轴相交于点D,其中![]() .
.
(1)分别求出A、B、C三点的坐标(可以用含有字母a的代数式表示).
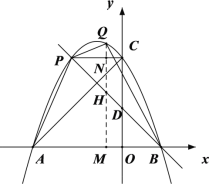
(2)点P与点C关于抛物线的对称轴成轴对称,点Q为抛物线上的一个动点.
①试说明点P在直线![]() 的图像上.
的图像上.
②若点Q在抛物线上有且只有三个位置满足![]() ,求a的值.
,求a的值.
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() 或
或![]()
【解析】
(1)令![]() 求解
求解![]() 的坐标,令
的坐标,令![]() 求
求![]() 的坐标;
的坐标;
(2)①根据抛物线是解析式求解抛物线的对称轴,由轴对称求解![]() 的坐标,把
的坐标,把![]() 的坐标代入
的坐标代入![]() 可得结论,②点Q在抛物线上有且只有三个位置满足
可得结论,②点Q在抛物线上有且只有三个位置满足![]() 得到
得到![]() 在在直线PB上方只能存在一个位置,即此时
在在直线PB上方只能存在一个位置,即此时![]() 的面积最大,利用函数的性质求解面积的最大值,分情况建立方程求解即可.
的面积最大,利用函数的性质求解面积的最大值,分情况建立方程求解即可.
(1)令![]() 则
则![]()
解得:![]()
![]()
令![]()
![]()
![]()
![]() A(-3,0)、B(a,0)、C(0,3)
A(-3,0)、B(a,0)、C(0,3)
(2)①![]()
![]() 抛物线的对称轴为
抛物线的对称轴为![]() ,
,
![]() 点P与点C关于抛物线的对称轴成轴对称,
点P与点C关于抛物线的对称轴成轴对称,
则中点坐标公式得:P坐标为(a-3,3)
将点P坐标(a-3,3)代入到![]() 中,得
中,得
![]() 成立
成立
∴点P在直线![]() 的图像上
的图像上
② 由题意得:![]()
在直线PB下方始终存在两个位置,使得![]()
则在直线PB上方只能存在一个位置,使得![]() ,
,
即![]() 最大时成立
最大时成立
由点Q在在直线PB上方,过点Q作x轴垂线,垂足为点M,
交PB于点H,交PC于点N,如图,则
![]()
![]() ,
,
![]()
![]() 设点
设点![]()
![]()
![]() 都在
都在![]() 上,
上,
![]() 为:
为:![]() ,
,
![]()
则![]()
当![]() 时,QH有最大值=
时,QH有最大值=![]() ,所以此时面积最大为
,所以此时面积最大为![]()
当![]() 时,
时,![]() ,得
,得
![]() ,则
,则![]()
当![]() 时,
时,![]() ,得
,得
![]() ,则
,则![]() (舍去)
(舍去)
综上所述:![]() 或
或![]()


科目:初中数学 来源: 题型:
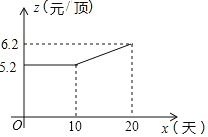
【题目】某企业接到一批帽子生产任务,按要求在20天内完成,约定这批帽子的出厂价为每顶8元.为按时完成任务,该企业招收了新工人,设新工人小华第x天生产的帽子数量为y顶,y与x满足如下关系式:y=![]()
(1)小华第几天生产的帽子数量为220顶?
(2)如图,设第x天每顶帽子的成本是P元,P与x之间的关系可用图中的函数图象来刻画.若小华第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大值是多少元?
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多49元,则第(m+1)天每顶帽子至少应提价几元?
查看答案和解析>>
科目:初中数学 来源: 题型:
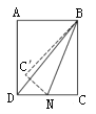
【题目】如图,在矩形ABCD中,AB=3,BC=4,点N为边DC上一动点(不与C、D重合),连接BN,作C关于直线BN的对称点C′连接B C′, C′N,当C′恰好在△ABD的边上时,CN的长为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
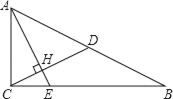
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
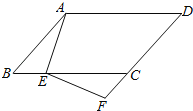
【题目】如图,在平行四边形ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.
(1)求证:△ABE∽△ECF;
(2)若AB=5,AD=8,BE=2,求FD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情后复学,某校为了了解九年级线上教学期间学生知识掌握情况,举行了线上教学质量调研测试,张老师根据测试结果,对本班部分学生进行了分析,他将结果分为四类,![]() :优秀;
:优秀;![]() :良好;
:良好;![]() :合格;
:合格;![]() :不合格,并将结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
:不合格,并将结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
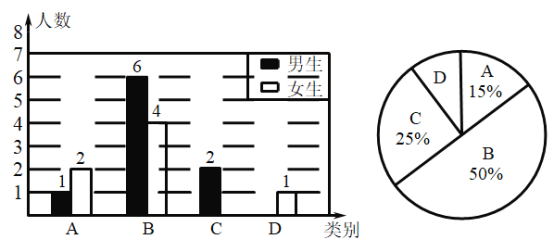
(1)张老师一共调查了_________名同学;
(2)![]() 类所占扇形圆心角的度数是_________;
类所占扇形圆心角的度数是_________;
(3)将上面条形统计图补充完整;
(4)为了共同进步,张老师想从被调查的![]() 类和
类和![]() 类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好都是女同学的概率.
类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好都是女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了运送防疫物资,甲、乙两货运公司各派出一辆卡车,分别从距目的地240千米和270千米的两地同时出发,驰援疫区.已知乙公司卡车的平均速度是甲公司卡车的平均速度的1.5倍,甲公司的卡车比乙公司的卡车晚1小时到达目的地,分别求甲、乙两货运公司卡车的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com